Latihan 4.2 Kekongruenan Dua Segitiga Hal Semester 2
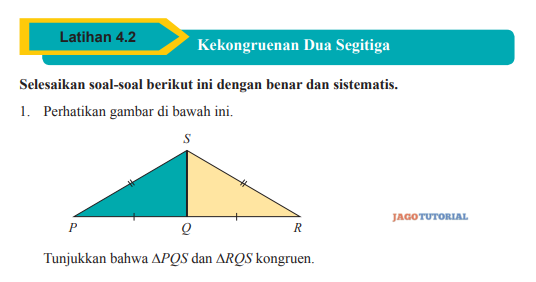
1. Perhatikan gambar di bawah ini. Tunjukkan bahwa ∆PQS dan ∆RQS kongruen.
2. Perhatikan gambar di bawah ini. Panjang AB = DE dan AB//DE. Tunjukkan bahwa ∆ABC dan ∆EDC kongruen.
3. Titik C adalah titik pusat lingkaran. Tunjukkan bahwa dua segitiga pada gambar di samping adalah kongruen.
4. Bangun WXYZ adalah segi empat dengan sisi-sisi yang berhadapan panjangnya sama.XY adalah salah satu diagonalnya.
A.Buktikan bahwa segitiga WXZ=segitiga ZYX
B.Tunjukkan bahwa WXYZ adalah jajargenjang.
5. Titik O adalah pusat lingkaran dalam dan lingkaran luar. AB adalah garis singgung dan titik P adalah titik singgung pada lingkaran kecil. Dengan menggunakan kekongruenan segitiga, tunjukkan bahwa titik P adalah titik tengah AB.
6. Pada segitiga abc , bm tegak lurus dengan ac , cn tegak lurus dengan ab . panjang bm sama dengan cn tunjukkan bahwa segitiga bcm samadengan segitiga cbn
7. titik M adalah titik tengah QR. Garis XM dan YM masing-masing tegak lurus pada PQ dan PR. Panjangn XM=TM. Buktikan bahwa segitiga QMX = segitiga RMY
8. Diketahui SR//PQ, OP=OQ, OS=OR. Ada berapa pasang segitiga yang kongruen? Sebutkan dian buktikan.
9. berpikir kritis.
apakah dua segitiga yang mempunyai tiga pasang sudut-sudut yang bersesuaian sama besar pasti kongruen? jelaskan dengan alasan yang mendukung jawabanmu.
10. Berpikir Kritis.
Apakah dua segitiga yang mempunyai dua pasang sisi yang bersesuaian sama panjang dan sepasang sudut yang bersesuaian sama besar pasti kongruen? Jelaskan dengan alasan yang mendukung jawabanmu.
11. Membagi Sudut
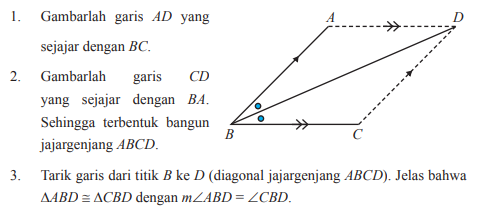
Gambarlah sebuah sudut dan beri nama ∠ABC, kemudian lakukan langkah berikut. a. Dengan menggunakan jangka, bagilah ∠ABC tersebut menjadi dua sama besar. b. Gambarlah lagi ∠ABC yang sama, kemudian tanpa menggunakan jangka maupun busur derajat, bagilah ∠ABC tersebut menjadi dua sama besar. (petunjuk: gunakan konsep segitiga kongruen)
12. Mengukur panjang danau. chan ingin mengukur sebuah danau tetapi tidak memungkinkan mengukurnya secara langsung.Dian merencanakan suatu cara yaitu ia memilih titik P,Q,R dan mengukur jarak QP dan RP.kemudian memperpanjang QP menuju ke Q dan RP menuju R sehingga panjang QP=PQ dan RP=PR.
chan menyimpulkan bahwa dengan mengukur panjang QR dia mendapatkan panjang danau tersebut.Apakah menurutmu strategi chan benar?jelaskan.
Kunci Jawaban Latihan 4.2 Kekongruenan Dua Segitiga Halaman 226 Semester 2
1. sisi-sisi yg sama panjang
PQ = RQ → (diketahui ada tanda)
QS (di Δ PQS) = QS (di Δ RQS) → (berhimpit)
PS = RS → (diketahui ada tanda)
sudut-sudut sama besar
∠ SPQ = ∠ QRS
∠ SQR = ∠ PQS
∠ PSQ = ∠ QSRKarena yang diketahui pada sisi-sisi
Jadi, Δ PQS dan Δ RQS adalah kongruen yang mempunyai kreteria sisi – sisi – sisi.
2. Pembuktian
AB = DE dan AB // DE
Sudut DCE = Sudut ACB (Sudut yang bertolak belakang)
Sudut ABC = Sudut CDE (Sudut yang berseberangan)
Hal-hal tersebut membuktikan bahwa Δ ABC dan Δ EDC adalah kongruen, dengan memenuhi kriteria SISI, SUDUT, SISI
3. sisi-sisi yg sama panjang
AB = DE
BC = CD → (diketahui jari-jari lingkaran)
AC = CE → (diketahui jari-jari lingkaran)
sudut-sudut sama besar
∠ ACB = ∠ DCE → (diketahui sudut bertolak belakang)
∠ ABC = ∠ CED = ∠ EDC = ∠ BACJadi, Δ ABC dan EDC adalah kongruen yg berdasarkan kretiria sisi – sudut – sisi.
4. a). ΔWXZ = ΔZYX karena diagonal WZ memotong segiempat WXZY sama besar
b). tidak ada bangun WXYZ.
tapi jika yang dimaksud adalah WXZY maka segiempat tersebut bisa jajar genjang, persegi, maupun persegi panjang dan belah ketupat.
5. Terdapat segitiga sama kaki AOB yang terbagi jadi dua segitiga yaitu Δ OAP dan Δ OBP dengan titik tengah di P.
P adalah titik singgung pada lingkaran kecil, maka OP tegak lurus dengan AB.
OA = OB merupakan jari-jari lingkaran (sisi diketahui)
∠ OAP = ∠ OBP (sudut diketahui)
∠ OPB = OPA merupakan sudut siku-siku (sudut diketahui)
Jadi Δ OAP dan Δ OBP adalah kongruen yg berdasarkan kriteria sisi – sudut – sudut.
6. Perhatikan bahwa segitiga BCM dan CBN adalah segitiga siku-siku yang memiliki sisi miring berimpit yaitu BC.
Diketahui bahwa BM = CN.
Akibatnya,
CM² = BC² – BM² = BC² – CN² = BN²
↔ CM² = BN²
↔ CM = BN
Artinya, sisi-sisi bersesuaian dari kedua segitiga memiliki panjang yang sama, sehingga memenuhi kaidah kekongruenan pada poin a.
Jadi, segitiga BCM dan segitiga CBN adalah dua segitiga yang sama dan sebangun (kongruen).
7. Pembuktian Δ QMX kongruen dg Δ RMY
Sisi yang sama panjang
QM = MR (diketahui, karena ada tanda)
XQ = YR
MX = MY
Sudut-sudut yang sama besar
∠ MXQ = ∠ MYR (diketahui, sudut siku-siku)
∠ XMQ = ∠ YMR (diketahui, sudut berimpit/beradu)
∠ MQX = ∠ MRY
Menentukan kreteria kita lihat yang diketahui pada gambar.
Jadi kreteria : sisi – sudut – sudut
8. Ada 3 pasang segitiga kongruen
∆ POS kongruen ∆ QOR
∆ PSR kongruen ∆ QRS
∆ PSQ kongruen ∆ QRP
9. Dua segitiga yang mempunyai tiga pasang sudut-sudut yang bersesuaian sama besar belum tentu Kongruen.Karena kita tidak tahu apakah sisi – sisinya yang bersesuain juga akan sama besar.Beda halnya dengan pernyataan bahwa dua segitiga yang mempunyai tiga pasang sisi yang bersesuaian sama besar pasti kongruen karena ketiga sudutnya juga pasti akan kongruen.Jadi yang mempengaruhi kekongruenan disini adalah sisi-sisinya.
10. syarat kekongruenan dan kesebangunan dua bangun datar adalah sisi sisi yang bersesuaian sama panjang dan sudut yang bersesuaian sama besar . jadi sudah pasti bahwa bangun tersebut kongruen
11. A. 1). Buat busur lingkaran dengan pusat titik B, sehingga memotong kaki sudut AB di titik D dan memotong kaki sudut BC di titik E.
2). Buat lagi 2 buah busur lingkaran masing-masing dengan pusat di titik D dan E. Perpotongan kedua busur lingkaran tersebut beri nama titik G.
3). Tarik garis dari titik B ke G, sehingga m∠ABG = ∠CBG.
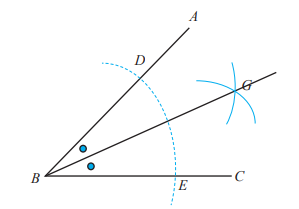
B.
12. Benar,karena chan menggunakan cara kekongruenan 2 segitiga,serta memenuhi kondisi sisi-sudut-sisi
Penjelasan :
RP=PR'(diketahui)
Sudut QPR=sudut Q’PR’ (bertolak belakang)
QP=PQ'(diketahui)






