
Latihan 4.4 Kesebangunan Dua Segitiga Semester 2
1. Pada gambar di samping, QR//ST.
a.Buktikan bahwa ΔQRP dan ΔTSP sebangun
b.Tuliskan perbandingan sisi-sisi yang bersesuaian?
2. Perhatikan gambar berikut.
ΔABC
Sisi AB =3 cm
Sisi AC =4 CM
ΔPQR
Sisi PR = 16 cm
Sisi RQ =20 cm
a.Buktikan bahwa ΔABC dan ΔPQR sebangun
b.Tuliskan perbandingan sisi-sisi yang bersesuaian?
3. Perhatikan gambar berikut.
Apakah ∆OLN sebangun dengan ∆OMN? Buktikan.
4. Pada ∆ABC dan ∆PQR diketahui m sudut A 105° sudut B 45° sudut P 45°dan sudut Q 105°
a. Apakah kedua segitiga tersebut sebangun ? Jelaskan.
b. Tuliskan pasangan sisi yang mempunyai perbandingan yang sama.
5. Diketahui sudut segitiga ABC=90derajat,siku siku di B
a. tunjukkan bahwa segitiga ADB dan segitiga ABC sebangun
b. tunjukan bahwa segitiga BDC dan segitiga ABC sebangun
6. A. tunjukkan bahwa segitiga FCE~segitiga ACB
b.tunjukkan bahwa segituga FCE~segitiga DEB
c.tunjukkan bahwa segitiga ACB~segitiga DEB
d.tentukan panjang FE dan AF
7. perhatikan gambar a. Hitunglah panjang EB b. Hitunglah panjang CE
8. Perhatikan gambar. hitunglah panjang MN pada gambar ini
9. Tentukan:
a. Pasangan segitiga yang sebangun.
b. Pasangan sudut yang sama besar dari masingmasing pasangan segitiga yang sebangun tersebut.
c. Pasangan sisi bersesuaian dari masing-masing pasangan segitiga yang sebangun tersebut.
d. Panjang sisi BA, BC, dan BD.
10. Dijetahui PR = 15 cm dan QU = 2/3 UP. tentukan panjang TS !
11. Diketahui KL = 10 cm dan MN = 14 cm. P dan Q berturut-turut adalah titik tengah LN dan KM. Tentukan panjang PQ
12. Segitiga ABC adalah segitiga siku-siku sama kaki. Jika AB = 10 cm dan CD garis bagi sudut C, Tentukan panjang BD.
13. Memperkirakan Tinggi Rumah Pada suatu sore, sebuah rumah dan pohon yang bersebelahan memiliki panjang bayangan berturut-turut 10 m dan 4 m. Jika tenyata tinggi pohon sebenarnya adalah 10 m, tentukan tinggi rumah tersebut sebenarnya.
14. Memperkirakan tinggi pohon: untuk menentukan tinggi sebuah pohon, Ahmad menempatkan cermin di atas tanah (dititik E).Dari titik E Ahmad berjalan mundur ke titik D, sedemikian hingga dia dapat melihat ujung pohon pada cermin. Ahmad mengukur panjang BE=18 m, ED=2,1 cm dan ketika berdiri jarak mata ahmad ke tanah (CD) adalah 1,4 m. perkirakan tinggi pohon
15. Memperkirakan Tinggi Bukit
Dua mahasisiwa Teknik Sipil Agung dan Ali ingin memperkirakan tinggi suatu bukit terhadap posisinya berdiri yang tidak jauh dari bukit itu. Mereka menggunakan bantuan peralatan laser yang dipasang pada sebuah tongkat penyangga setinggi 3 m dari permukaan tanah. Agung mengamati puncak bukit melalui alat tersebut dan diperoleh garis pandang ke puncak bukit adalah 1.540 m. Ali berbaring di tanah memandang ke arah ujung peralatan tersebut dan puncak bukit sehingga tampak sebagai garis lurus. Posisi mata Ali berjarak 4 m dari tongkat penyangga. Perkirakan tinggi bukit tersebut. (perhatikan gambar)
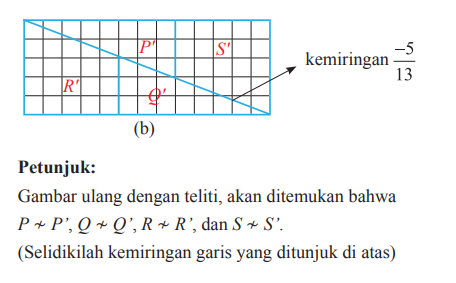
16. Analisis Kesalahan Gambar (a) menunjukkan persegi dengan panjang sisi 8 satuan. Persegi itu dibagi menjadi 4 bagian yaitu dua segitiga (P dan Q), serta dua trapesium (R dan S). Gambar (b) menunjukkan persegi panjang berukuran 5 satuan × 13 satuan. Persegi itu dibagi menjadi 4 bagian yaitu dua segitiga (P’ dan Q’), serta dua trapesium (R’ dan S’). Apakah 8 × 8 = 5 × 13? Jika tidak, bagaimana kamu menjelaskan hal ini? Di mana letak kesalahannya?
17. Analisis Kesalahan
Perhatikan gambar di bawah ini! Jelaskan di manakah letak kesalahannya?
Jelaskan dari manakah lubang satu kotak ini berasal?
Kunci Jawaban Latihan 4.4 Kesebangunan Dua Segitiga Halaman 254 Semester 2
1. sudut QPR = sudut SPT (bertolak belakang)
sudut PQR = sudut STP (dalam berseberangan)
sudut PRQ = sudut PST (dalam berseberangan)
karena ketiga sudut yang bersesuaian besarnya sama maka :Δ QRP sebangun dengan Δ TPS (terbukti)
b) QR : ST = PR : PS = PQ : PT
2. Perhatikan segitiga warna hijau
Panjang sisi yang mengapit sudut 90 adalah 3 cm dan 4 cm.
Kita cari panjang sisi miringnya (BC) dengan teorema pythagoras
BC² = AB² + AC²
= 3² + 4²
= 9 + 16
= 25
BC = √25
= 5 cm
Perhatikan segitiga warna kuning
Panjang sisi miring (QR) = 20 cm
Panjang PR = 16 cm
Kita cari panjang PQ dengan teorema pythagoras
PQ² = QR² – PR²
= 20² – 16²
= 400 – 256
= 144
PQ = √144
= 12 cm
Kita lihat perbandingan panjang sisi pada kedua segitiga itu
Pada segitiga ABC
AB : AC : BC = 3 : 4 : 5
Pada segitiga PQR
PQ : PR : QR = 12 : 16 : 20 kita kecilkan perbandingan dengan membagi FPB dari 12, 16 dan 20 yaitu dengan 4
= (12:4) : (16:4) : (20:4)
= 3 : 4 : 5
Ternyata perbandingan panjang sisi- panjang sisinya sama, maka kedua segitiga tersebut adalah sebangun
Perbandingan sisi yang bersesuaian
AB : PQ = AC : PR = BC : QR
3. bukti
sudut LON = sudut MKN (siku”)
sudut OLN = sudut KMN (dalam berseberangan)
sudut ONL -= sudut KNM (berhimpit atau bersekutu)
karena ketiga sudut tang bersesuaian besarnya sama maka ..
Δ OLN sebangu dengan Δ KMN (terbukti)
4. a. Pembuktian kedua segitiga tersebut sebangun
Sudut-sudut yang sama besar
• ∠ A = ∠ Q = 105°
• ∠ B = ∠ P = 45°
• ∠ C = ∠ R = 180° – 105° – 45° = 30°
Iya, kedua segitiga tersebut sebangun karena dua pasang sudut yang bersesuaian sama besar.
Untuk gambar dua segitiga sebangun bisa dilihat pada lampiran.
b. Pasangan sisi yang mempunyai perbandingan yang sama
• AB dengan QP
• BC dengan PR
• AC dengan QR
5. a. Perhatikan sudut-sudut bersesuaian pada segitiga ADB dan segitiga ABC.
sudut BAD = sudut BAC (kedua sudut berimpit)
sudut ADB = sudut ABC (kedua sudut merupakan sudut siku-siku)
sudut ABD = 180° – sudut BAD – sudut ADB
= 180° – sudut BAC – sudut ABC
= sudut ACB
Karena ketiga pasang sudut bersesuaian sama besar, maka segitiga ADB sebangun dengan segitiga ABC.
b. Dengan cara yang sama seperti poin a.
Perhatikan sudut-sudut bersesuaian pada segitiga BDC dan segitiga ABC.
sudut BCD = sudut BCA (kedua sudut berimpit)
sudut BDC = sudut ABC (kedua sudut merupakan sudut siku-siku)
sudut CBD = 180° – sudut BCD – sudut BDC
= 180° – sudut BCA – sudut ABC
= sudut BAC
Karena ketiga pasang sudut bersesuaian sama besar, maka segitiga BDC sebangun dengan segitiga ABC.
6. • a. Tunjukkan bahwa Δ FCE ~ Δ ACB
Sisi-sisi yang bersesuaian
FC dengan AC
CE dengan BC
FE dengan AB
Sudut-sudut sama besar
∠ CFE = ∠ CAB (sudut sehadap)
∠ CEF = ∠ CBA (sudut sehadap)
∠ FCE = ∠ ACB (sudut berimpit)
• b. Tunjukkan bahwa Δ FCE ~ Δ DEB
Sisi-sisi yang bersesuaian
FC dengan DE
CE dengan BE
FE dengan DB
Sudut-sudut sama besar
∠ CFE = ∠ EDB (sudut sehadap)
∠ CEF = ∠ DBE (sudut sehadap)
∠ FCE = ∠ DEB (sudut sehadap)
• c. Tunjukkan bahwa Δ ACB ~ Δ DEB
Sisi-sisi yang bersesuaian
AC dengan DE
BC dengan BE
AB dengan DB
Sudut-sudut sama besar
∠ CAB = ∠ BDE (sudut sehadap)
∠ ABC = ∠ DBE (sudut berimpit)
∠ ACB = ∠ DEB (sudut sehadap)
d. Perhatikan segitiga FCE dengan segitiga DEB.
FE : DB = CE : EB
↔ FE : 12 = 5 : 10
↔ FE = 12 × 5 : 10 = 6 cm
ED : CF = EB : CE
↔ ED : 4 = 10 : 5
↔ ED = 4 × 10 : 5 = 8 cm
Perhatikan bahwa AF = ED = 8 cm
Jadi, FE = 6 cm dan AF = 8 cm
7. a. Misal panjang EB = x
Dengan menggunakan perbandingan, maka:
5/7 = 6/(6+x)
<=> 5(6+x) = 6(7)
<=> 30 + 5x = 42
<=> 5x = 42 – 30
<=> 5x = 12
<=> x = 12/5
<=> x = 2,4
b. Dengan menggunakan perbandingan, maka:
4/6 = 8/(4+CE)
<=> 4(4+CE) = 6 x 8
<=> 16 + 4CE = 48
<=> 4CE = 48 – 16
<=> 4CE = 32
<=> CE = 32/4
<=> CE = 8
8. Kita lihat ΔTQR
Sisi-sisi bersesuaian memiliki perbandingan sama, sehingga
RQ/RT = ON/TQ
5/8 = ON/8
⇔ ON = 5/8 x 8
⇔ ON = 5
Jadi, panjang ON adalah 5 cm.
MN = MO + ON
⇔ MN = 12 + 5
⇔ MN = 17
Jadi, panjang MN adalah 17 cm.
9. a). segitiga ABC ~ segitiga ADB ~ segitiga BDC
b). sudut CBA = sudut BDA = sudut CDB
sudut BAC = sudut DAB = sudut DBC
sudut ACB = sudut ABD = sudut BCD
c). BC~DB~DC
AC~AB~BC
AB~AD~BD
d). BD²= DA×DC
BD²= 32×18
BD = √576 = 24 cm
BC²= CD×CA
BC²= 18×50
BC = √900 = 30 cm
BA²= AD×AC
BA²= 32×50
BA = √1600 = 40 cm
10. PR/UT = QP/QU
15/UT = (2/3UP + UP)/ 2/3 UP
15/UT = 5/2
5 UT = 30
UT = 6 cm
selanjutnya cari panjang TS
PR = US = UT + TS
15 = 6 + TS
TS = 9 cm
Jadi panjang TS adalah 9 cm
PQ = (14-10)/2 = 4/2 = 2 cm
AB = CB = EC = 10 cm
BD = DE = AE
perbandingan sudut 45° (segitiga sama kaki siku-siku) = s : m = 1 : √2
11. AB : AC = 1 : √2
10/AC = 1/√2
AC = 10√2 cm
BD = AC – EC
BD = (10√2 – 10) cm
= 10 (√2 – 1) cm
12. Dik :
T.bayangan rumah = 10 m
T.bayangan pohon = 4m
T.sbenarnya pohon = 10 m
Dit :
T.sbenarnya rumah….?
Jawab :
Tb pohon / Ts pohon = Tb rumah / Ts rumah
4/10 = 10/Ts rumah
4Tsrumah = 100
Tsrumah = 100/4
Tsrumah = 25 m
13. Diketahui:
Jarak Ahmad ke cermin = ED = 2,1 m.
Tinggi mata Ahmad = CD = 1,4 m
Jarak dari cermin ke pohon = BE = 18 m
Ditanyakan:
tinggi pohon = ?
Jawab:
Tinggi pohon : Tinggi mata Ahmad = Jarak pohon ke cermin : jarak Ahmad ke cermin
↔ AB : CD = BE : ED
↔ AB : 1,4 = 18 : 2,1
↔ AB = 1,4 × 18 : 2,1 = 12
Jadi tinggi pohon adalah 12 m
14. jarak pandang dengan ujung tongkat
a = √4² + 3²
a = √16 + 9
a = √25
a = 5
sudut Pandang Ali dengan tongkat
sin A = 3/5
jarak pandang Ali dengan bukit = 1.540 + 5 = 1.545
15. Tinggi bukit
Tinggi Bukit/Jarak Pandang Ali = Sin A
Tinggi Bukit/1.545 = 3/5
Tinggi Bukit = 1.545 x 3/5
Tinggi Bukit = 927 m
16.

17.

Jadi selisih luas= 12 – 10,5 = 1,5 satuan kotak
dibulatkan menjadi 1 satuan kotak
Sehingga terbukti bahwa segitiga merah pada (ii) lebih kecil 1 kotak daripada segitiga merah pada (i), sehingga jelas luas bangun pada gambar (ii) lebih kecil 1 satuan kotak daripada luas bangun (i)






