
SOAL DAN PEMBAHASAN BUKU SISWA MATEMATIKA KELAS 8 SEMESTER 2 LATIHAN 6.3 HALAMAN 31 TAHUN 2021
- Manakah diantara kelompok tiga bilangan yang membentuk segitiga siku siku ,
segitiga lancip,dan segitiga tumpul?
a. 13,9,11
b. 8,17,15
c. 130,120,50
d. 12,6,5
e. 10,20,24
f. 18,22,12
g. 1,73;2,23;1,41
h. 12,36,35
Pembahasan:
Yang merupakan segitiga siku-siku adalah :
b. 17² = 8² + 15²
289 = 64 + 225
289 = 289
c. 130² = 120² + 50²
16900 = 14400 + 2500
16900 = 16900
Yang merupakan segitiga lancip :
a. 13² < 9² + 11²
169 < 81 + 121
169 < 202
g. 2,23² < 1,41² + 1,73²
4,9729 < 1,9881 + 2,9929
4,9729 < 4,981
h. 36² < 12² + 35²
1296 < 144 + 1225
1296 < 1369
Yang merupakan segitiga tumpul adalah
d. 16² > 12² + 5
256 > 144 + 25
256 > 169
e. 24² > 20² + 10²
576 > 400 + 100
576 > 500
f. 22² > 18² + 12²
484 > 324 + 144
484 > 468- Manakah diantara kelompok tiga bilangan berikut yang merupakan
tripel pythagoras?
a. 10,12,14
b. 7,13,11
c. 6, 2 1/2 , 6 ½
Pembahasan:
a. 10² + 12² ... 14²
100 + 144 ... 196
244 >196
Bukan tripel phytagoras
b. 7² + 11² ... 13²
49 + 121 ... 169
170 > 169
Bukan tripel phytagoras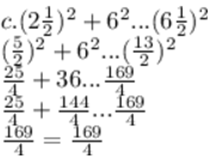
Merupakan tripel phytagoras
Jadi, kelompok 3 bilangan yang memenuhi tripel phytagoras adalah no c
- Tentukan apakah segitiga KLM dengan titik K(6,-6), L(39,-12), dan M(24,18) adalah
segitiga sembarang, segitiga sama kaki, atau segitiga sama sisi. jelaskan pendapatmu!
Pembahasan:
Kita cari panjang sisi-sisinya terlebih dahulu, dengan menggunakan rumus pythagoras
c = √(a² + b²)
Dengan c sisi terpanjang (sisi miring)
Kita cari panjang KL
KL = √{(y2 - y1)² + (x2-x1)²}
KL = √{(-12-(-6))² + (39 - 6)²}
KL = √{(-6)² + 33²}
KL = √(36 + 1089)
KL = √1125
KL = 33,5 satuan
Kita cari panjang KM
KM = √{(y2 - y1)² + (x2-x1)²}
KM = √{(18-(-6)² + (24-6)²}
KM = √(24² + 18²)
KM = √(576 + 324)
KM = √900
KM = 30 satuan
Kita cari panjang LM
LM = √{(y2 - y1)² + (x2-x1)²}
LM = √{(18-(-12)² + (24-39)²}
LM = √{30² + (-15)²}
LM = √(900 + 225)
LM = √1125
LM = 33,5 satuan
Karena ada dua sisi yang sama panjangnya yaitu sisi KL dan LM, sehingga dapat
disimpulkan bahwa segitiga KLM adalah segitiga sama kaki- Jika 32, x, 68 adalah tripel Pythagoras . Berapakah nilai x?
Tunjukan bagaimana kalian mendapatkannya.
Pembahasan:
Diketahui panjang sisi-sisi suatu segitiga, yaitu
a = 32, b = x, dan c = 68.
Dengan menggunakan rumus Pythagoras, diperoleh
a² + b² = c²
⇔ 32² + x² = 68²
⇔ x² = 68² - 32²
⇔ x² = 4.624 - 1.024
⇔ x² = 3.600
⇔ x = √3.600
⇔ x = √60²
⇔ x = 60
Jadi, jika 32, x, 68 adalah Tripel Pythagoras, maka x adalah 60.- Bilangan terkecil dari tripel pythagoras adalah 33. Tentukan tripel pythagoras.
Jelaskan bagaimana kalian menemukan dua bilangan lainnya.
Pembahasan:
Diketahu bilangan terkecil tripel pythagoras adalah 33.
Karena bilangan terkecil adalah kelipatan 3, maka dapat dibandingkan dengan
bilangan tripel pythagoras dengan bilangan terkecil 3.
Sudah diketahui bahwa (3,4,5) adalah bilangan tripel pythagoras sehingga
untuk setiap x bilangan bulat positif, bilangan-bilangan (3x, 4x, 5x)
juga merupakan tripel pythagoras.
Jadi
a = 3 . 11 = 33
b = 4 . 11 = 44
c = 5 . 11 = 55
Sehingga didapatkan
332 + 442 = 552
1089 + 1936 = 3025
3025 = 3025 merupakan tripel Pythagoras.
Jadi dua bilangan lainnya adaalah 44 dan 55.- Bingkai jendela yang terlihat berbentuk persegi panjang dengan tinggi 408 cm,
panjang 306 cm, dan panjang salah satu diagonalnya 525 cm.
Apakah bingkai jendela tersebut benar benar persegi panjang? Jelaskan.

Pembahasan:
Segiempat disebut persegi panjang jika panjang, lebar dan diagonalnya membentuk tripel pythagoras.
d2 = p² + l²
5252 = 306² + 408²
275.625 = 93.636 + 166.464
275.625 = 260.100
260.100 tidak sama dengan 275.625
Karena tidak sama dengan, maka bukan persegi panjang- Panjang sisi-sisi segitiga adalah 1 cm, 2a cm, dan 3a cm. Buktikan bahwa
ketiga ukuran tersebut bukan merupakan triple Pythagoras.
a. Jika (p – q), p, (p + q) membentuk triple phytagoras, tentukan hubungan antara p dan q
b. Jika p = 8, tentukan triple Pythagoras.
Pembahasan:
Panjang sisi-sisi segitiga adalah 1 cm, 2a cm, dan 3a cm. Buktikan bahwa
ketiga ukuran tersebut bukan merupakan triple Pythagoras.
1² + (2a)² ... (3a)²
1 + 4a² ... 9a²
1 + 4a² ≠ 9a²
Sehingga ketiga ukuran tersebut bukan merupakan triple Phytagoras
a. Jika (p - q), p, (p + q) membentuk triple phytagoras, tentukan hubungan antara p dan q
(p - q)² + p² = (p + q)²
p² - 2pq + q² + p² = p² + 2pq + q²
p² - 2pq + q² + p² - p² - 2pq - q² = 0
p² - 4pq = 0
p (p - 4q) = 0
p = 0 atau p - 4q = 0
p = 0 atau p = 4q
p = 0 tidak memenuhi, maka p = 4q
b. Jika p = 8, tentukan triple Pythagoras
p = 8 substitusikan ke persamaan p = 4q
p = 4q
8 = 4q
q = 8/4 = 2
(p - q) = 8 – 2 = 6
p = 8
(p + q) = 8 + 2 = 10
Jadi terbukti triple Phytagoras : 6 ,8, 10- Perhatikan segitiga ABC berikut ini. BD = 4cm, AD = 8cm, dan CD = 16cm.
a. Tentukan panjang AC
b. Tentukan panjang AB
c. Apakah segitiga ABC adalah segitiga siku? Jelaskan.
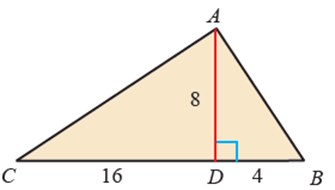
Pembahasan:
a. Perhatikan Δ ADC
AC² = CD² + AD²
AC² = 16² + 8²
AC² = 256 + 64
AC² = 320
AC = √320
AC = √64 x √5
AC = 8√5 cm
Jadi panjang AC adalah 8√5 cm
b. Perhatikan Δ ADB
AB² = BD² + AD²
AB² = 4² + 8²
AB² = 16 + 64
AB² = 80
AB = √80
AB = √16 x √5
AB = 4√5 cm
Jadi panjang AB adalah 4√5 cm
c. Pembuktian apakah Δ ABC merupakan segitiga siku-siku
dengan mengguanakan pythagoras.
BC² = AC² + AB²
(16 + 4)² = (8√5)² + (4√5)²
20² = (64 × 5) + (16 × 5)
400 = 320 + 80
400 = 400
Karena hasilnya sama dengan, maka Δ ABC adalah siku-siku.- Diketahui persegi panjang ABCD. Terdapat titik P sedemikian sehingga
PC = 8cm, PA = 6cm, dan PB = 10cm. Dapatkah kalian menentukan jarak
titik P dan D? Bagaimana kalian menentukanya?
Pembahasan:
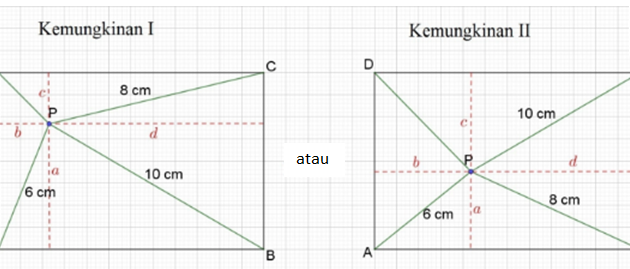
Kemungkinan I :
Diketahui :
PC = 8 cm
PA = 6 cm
PB = 10 cm
Pada gambar persegi panjang ABCD, kita lihat
∠ APB, ∠ BPC, ∠ CPD dan ∠ APD tidak ada yang siku-siku.
Jadi Δ CPD dan Δ APB tidak bisa kita pythagoraskan langsung.
Kita tarik garis merah yang tegak lurus melalui titik P agar terbentuk
segitiga siku-siku, karena syarat pythagoras adalah salah satu sudut
pada segitiga haruslah siku-siku dan kedua sisi tegak lurus.
Ada 4 garis diagonal yang terdiri dari 4 segitiga siku-siku
Keempat diagonal tersebut kita masukan kedalam rumus pythagoras
yaitu c² = a² + b², maka PD² = b² + c²
PA² = a² + b²
6² = a² + b²
b² = 6² - a²
PB² = a² + d²
10² = a² + d²
d² = 10² - a²
PC² = c² + d²
8² = c² + d²
c² = 8² - d²
PD² = b² + c²
PD² = (6² - a²) + (8² - d²)
PD² = 6² - a² + 8² - (10² - a²)
PD² = 6² - a² + 8² - 10² + a²
PD² = 6² + 8² - 10²
PD² = 36 + 64 - 100
PD² = 100 - 100
PD = 0
Karena hasilnya nol kemungkinan ada kekeliruan pada soal.
Kemungkinan II :
Saya akan menukarkan ukurannya antara PC dan PB
Diketahui :
PC = 10 cm
PA = 6 cm
PB = 8 cm
Ditanya :
PD = ... ?
Jawab :
PA² = a² + b²
6² = a² + b²
b² = 6² - a²
PB² = a² + d²
8² = a² + d²
d² = 8² - a²
PC² = c² + d²
10² = c² + d²
c² = 10² - d²
PD² = b² + c²
PD² = (6² - a²) + (10² - d²)
PD² = 6² - a² + 10² - (8² - a²)
PD² = 6² - a² + 10² - 8² + a²
PD² = 6² + 10² - 8²
PD² = 36 + 100 - 64
PD² = 136 - 64
PD² = 72
PD = √72
PD = √36 x √2
PD = 6√2 cm
Jadi jara k titik P dan D adalah 6√2 cm
cara cepat :
PD² + PB² = PA² + PC²
PD² + 8² = 6² + 10²
PD² = 6² + 10² - 8²
PD² = 36 + 100 - 64
PD² = 136 - 64
PD² = 72
PD = √72
PD = 6√2 cm
Jadi jara k titik P dan D adalah 6√2 cmSelamat belajar semoga bermanfaat.







