Ayo Kita Berlatih 6.1 Semester 2
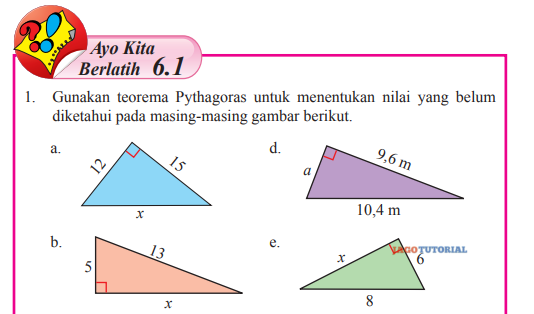
1. Gunakan teorema Pythagoras untuk menentukan nilai yang belum diketahui pada masing-masing gambar berikut.
2. Tujuan dipasangkan kawat bubut pada suatu tiang telepon adalah untuk menopangnya. Kawat bubut dipasang pada tiang telepon setinggi 8 meter dari tanah.
a. Jelaskan cara yang akan kalian lakukan untuk menentukan panjang kawat bubut tanpa mengukur langsung kawat tersebut.
b. Tentukan panjang kawat jika jarak antara kawat dan tiang pada tanah adalah 6 meter.
3. Tentukan nilai x pada kedua gambar berikut.
4. Apakah suatu segitiga yang panjang ketiga sisinya berturut-turut 9 cm,12 cm, dan 18 cm merupakan segitiga siku-siku? Jelaskan.
5. Jika panjang sisi-sisi suatu segitiga siku-siku berturut-turut adalah x, 15, dan x + 5, tentukan nilai x.
6. Tentukan panjang AB dari gambar berikut.
7. Diketahui persegi panjang ABCD dan P merupakan titik di dalam persegi panjang. Jika PC = 8 cm, PD = 4 cm, dan PB = 7 cm, maka PA adalah ….
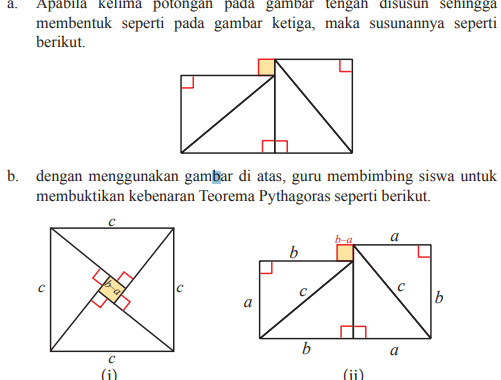
8. Seorang yang bernama Bhaskara menyusun sebuah persegi dan empat buah segitiga siku-siku yang memiliki panjang sisi yang sama yaitu a, b dan c kedalam sebuah persegi yang mempunyai panjang sisi c.
a. Tunjukkan bagaimana kelima potong bangun datar yang disusun pada gambar bagian tengah dapat disusun untuk mengisi bangun yang paling kanan.
b. Jelaskan bagaimana teorema Pythagoras termuat dalam pertanyaan a.
9. perhatikan gambar dua persegi di samping. panjang sisi persegi besar adalah 15 cm. luas persegi kecil adalah 25 cm². tentukan nilai x
10. diketahui ABC siku siku di B dengan panjang AC=40 cm dan BC=24 cm.Titik D terletak pada AB sedemikian sehingga CD=25 cm.Panjang AD adalah
Kunci Jawaban Ayo Kita Berlatih 6.1 Halaman 11 Semester 2
1. a. Diketahui a = 12 cm dan b = 15 cm, sehingga
a² + b² = c²
⇔ 12² + 15² = c²
⇔ 144 + 225 = c²
⇔ c² = 369
⇔ c = √(9 x 41)
⇔ c = 3√41
Jadi, nilai c = 3√41 cm.
b. Diketahui nilai a = 5 cm dan c = 13 cm, sehingga
a² + b² = c²
⇔ 5² + x² = 13²
⇔ 25 + x² = 169
⇔ x² = 169 – 25
⇔ x² = 144
⇔ x = 12
Jadi, nilai b = x = 12 cm.
c. Diketahui nilai b = 5,6 inchi dan c = 10,6 inchi, sehingga
a² + b² = c²
⇔ a² + 5,6² = 10,6²
⇔ a² + 31,36 = 112,36
⇔ a² = 112,36 – 31,36
⇔ a² = 81
⇔ a = 9
Jadi, nilai a = 9 inchi.
d. Diketahui b = 9,6 m dan c = 10,4 m.
a² + b² = c²
⇔ a² + 9,6² = 10,4²
⇔ a² + 92,16 = 108,16
⇔ a² = 108,16 – 92,16
⇔ a² = 16
⇔ a = 4
Jadi, nilai a = 4 m.
e. Diketahui b = 6 m dan c = 8 m, sehingga
a² + b² = c²
⇔ a² + 6² = 8²
⇔ x² + 36 = 64
⇔ x² = 64 – 36
⇔ x² = 28
⇔ x = √(4 x 7)
⇔ x = 2√7
Jadi, nilai a = x = 2√7 m.
f. Diketahui a = 9,6 kaki dan b = 7,2 kaki, sehingga
a² + b² = c²
⇔ 9,6² + 7,2² = c²
⇔ 92,16 + 51,84 = c²
⇔ c² = 144
⇔ c = 12
Jadi, nilai c = 12 kaki.
2. a. Tanah yang datar dan tiang listrik membentuk sudut siku-siku, maka bangun yang terbentuk adalah segitiga siku-siku.
Pada segitiga siku-siku bisa kita terapkan pyhtagoras untuk mencari panjang sisi yg lain tanpa harus mengukur langsung.
b. misalkan : a = tinggi tiang yg dipasang kawat dari tanah
b = jarak pada tanah
c = panjang kawat bubut
c² = a² + b²
c² = 8² + 6²
= 64 + 36
= 100
c = √100
c = 10 m
Jadi panjang kawat bubut adalah 10 m
3. Diketahui:
Sisi Miring (sisi terpanjang) = 20 cm → c
Sisi lainnya = 12 cm → a
Ditanya:
Nilai x = … ? → b
Jawab:
Untuk menyelesaiakan gunakan rumus teorema Pythagoras.
a² + b² = c²
12² + x² = 20²
144 + x² = 400
x² = 400 – 144
x² = 256
x = √256
x = 16 cm
4. Diketahui a = 9 cm, b = 12 cm, dan c = 18 cm.
a² + b² = c²
⇔ 9² + 12² = c²
⇔ 81 + 144 = c²
⇔ c² = 225
⇔ c = 15
Jadi, suatu segitiga yang panjang ketiga sisinya berturut-turut 9 cm, 12 cm, dan 18 cm bukan segitiga siku-siku.
5. Diketahui:
Sisi” segitiga siku” adalah x, 15 dan x + 15
Ditanya:
Nilai x = … ?
Jawab:
Penyelesaian soal ini menggunakan teorema pythagoras
a² + b² = c²
x² + 15² = (x + 5)²
x² + 225 = x² + 10x + 25
x² – x² – 10x = 25 – 225
-10x = -200
x = -200 : -10
x = 20
Jadi Nilai x adalah 20
6. • Gambar a.
Diketahui :
AD = CD = 4 cm
BC = 3 cm
Panjang AB
AB² = (AD – BC)² + CD²
= (4 – 3)² + 4²
= 1 + 16
= 17
AB = √17
Jadi panjang AB gambar a adalah √17 cm
• Gambar b
Diketahui :
CD = 4 cm
BC = 7 cm
AD = 6 cm
Panjang BD pada segitiga BCD
BD² = BC² + CD²
= 7² + 4²
= 49 + 16
= 65
BD = √65
Panjang AB pada Δ ABD
AB² = BD² – AD²
= (√65)² – 6²
= 65 – 36
= 29
AB = √29
Jadi panjang AB gambar b adalah √29 cm
• Gambar c
Diketahui :
AO = 3 cm + 1 cm = 4 cm
BO = 5 cm
Panajang AB
AB² = AO² + BO²
= 4² + 5²
= 16 + 25
= 41
AB = √41
Jadi panjang AB gambar c adalah √41 cm
7. PA² + PC² = PD² + PB²
PA² + 8² = 4² + 7²
PA² = 4² + 7² – 8²
PA² = 16 + 49 – 64
PA² = 65 – 64
PA² = 1
PA = 1 cm
8.

9. Garis x merupakan hipetenusa dari dua sisi siku-siku yaitu sisi AB dan BC.
• Menentukan panjang sisi persegi kecil
L persegi kecil = 25 cm²
L = s²
s = √L
s = √25
s = 5 cm
Jadi panjang sisi persegi kecil = 5 cm
• Menentukan nilai x menggunakan pythagoras
x² = AB² + BC²
x² = 15² + (15 + 5)²
x² = 15² + 20²
x² = 225 + 400
x² = 625
x = √625
x = 25 cm
Jadi nilai x aadalah 25 cm
10. Panjang AB dapat diketahui dengan theorema phythagoras sebagai berikut.
AB = √(AC² – BC²)
= √(40² – 24²)
= √(1600 – 576)
= √1024
AB = 32 cm
Lalu, kita hitung panjang BD juga dengan theorema phythagoras.
BD = √(CD² – BC²)
= √(25² – 24²)
= √(625 – 576)
= √49
BD = 7 cm
Setelah mengetahui panjang AB dan BD, kita akan menentukan panjang AD.
AD = AB – BD
= 32 cm – 7 cm
= 25 cm
Jadi, panjang AD adalah 25 cm.






