Latihan 5.3 Bola Semester 2
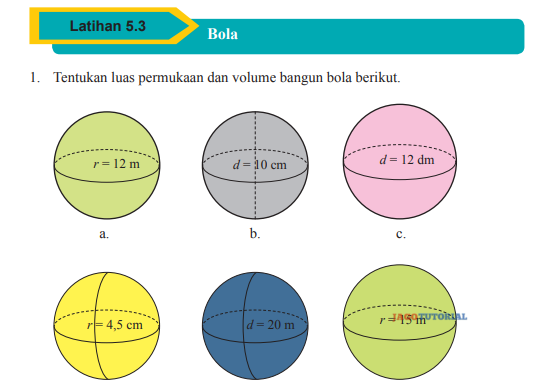
1. Tentukan luas permukaan dan volume bangun bola berikut.
2. Tentukan luas permukaan bangun setengah bola tertutup berikut :
a = 8 cm
b= 12 cm
c = 12 cm
d= 8 m
e= 15 m
f= 11 dm
3. Dari soal-soal nomor 2 tentukan rumus untuk menghitung luas permukaan setengah bola tertutup.
4. Tentukan jari-jari dari bola dan setengah bola tertutup
a.L=729πcm²
b.V=2.304π cm²
c.V=36π cm²
d.L=27π m²
e.L=45π m²
f.V=128/3π m²
5. Berpikir kritis. tedapat suatu bola dengan jari jari r cm. jika luas permukaan bola tersebut adalah a cm³ dan volume bola tersebut adalah A cm³. tentukan:
a. nilai r
b. nilai a
6. Bangun disamping dibentuk dari dua setengah bola yang sepusat. setengah bola yang lebih kecil memiliki jari jari r1=4cm sedangkan yang lebih besar memiliki jari jari r2=8cm
tentukan:
a. luas permukaan bangun tersebut
b. volume bangun tersebut
7. Analisis kesalahan. Lia menghitung luas permukaan bola dengan cara membagi volume bola dengan jari-jari bola tersebut (L = V/r ). Tentukan kesalahan yang dilakukan oleh Lia.
8. Bola di dalam kubus. Terdapat suatu kubus dengan S panjang sisi s cm. Dalam kubus tersebut terdapat bola dengan kondisi semua sisi kubus menyentuh bola (lihat gambar di samping).
a. Tentukan luas permukaan bola tersebut.
b. Tentukan volume bola tersebut.
Petunjuk: tentukan jari-jari bola terlebih dahulu.
9. Kubus di dalam bola. Terdapat suatu kubus S dengan panjang sisi s cm. Kubus tersebut berada di dalam bola dengan kondisi semua titik sudut kubus menyentuh bola.
a. Tentukan luas permukaan bola tersebut
b. Tentukan volume bola tersebut
Petunjuk: tentukan jari-jari bola terlebih dahulu.
10. Timbangan dan kelereng. Andi punya dua macam kelereng. Kelereng tipe I berjari-jari 2 cm sedangkan tipe II berjari-jari 4 cm. Andi melakukan eksperimen dengan menggunakan timbangan. Timbangan sisi kiri diisi dengan kelereng tipe I sedangkan sisi kanan diisi dengan kelereng tipe II. Tentukan perbandingan banyaknya kelereng pada sisi kiri dengan banyaknya kelereng pada sisi kanan agar timbangan tersebut seimbang.
Kunci Jawaban Latihan 5.3 Bola Halaman 303 Semester 2
1. a. Luas dan volume bola jika panjang jari jari (r) = 12 m adalah 1.808,64 m² dan 7.234,56 m³.
Jawab :
HITUNG LUAS BOLA (L)
L = 4πr²
Keterangan: L = luas permukaan bola
r = jari – jari bola
π = ²²/₇ atau 3,14
Penyelesaiannya :
L = 4πr²
= 4 × 3,14 × (12 m)²
= 4 × 3,14 × 144 m²
= 1.808,64 m²
HITUNG VOLUME BOLA (V)
V = ⁴/₃ πr³
Keterangan : V = volume bola (cm³)
π = ²²/₇ atau 3,14
r = jari jari bola (cm)
Penyelesaiannya :
V = ⁴/₃ πr³
= ⁴/₃ × 3,14 × (12 m)³
= ⁴/₃ × 3,14 × 1.728 m³
= 7.234,56 m³
b. Luas dan volume bola jika diameter (d) = 10 cm adalah 314 cm² dan 523,33 cm³.
Jawab :
HITUNG PANJANG JARI JARI (r)
r = ¹/₂ × d
Keterangan :
r = jari – jari bola
d = diameter bola
Penyelesaiannya :
r = ¹/₂ × d
r = ¹/₂ × 10 cm
r = 5 cm
HITUNG LUAS BOLA (L)
L = 4πr²
= 4 × 3,14 × (5 cm)²
= 4 × 3,14 × 25 cm²
= 314 cm²
HITUNG VOLUME BOLA (V)
V = ⁴/₃ πr³
= ⁴/₃ × 3,14 × (5 cm)³
= ⁴/₃ × 3,14 × 125 cm³
= 523,33 cm³
c. Luas dan volume bola jika diameter (d) = 12 cm adalah 452,16 cm² dan 904,32 cm³.
Jawab :
HITUNG PANJANG JARI JARI (r)
r = ¹/₂ × d
Keterangan :
r = jari – jari bola
d = diameter bola
Penyelesaiannya :
r = ¹/₂ × d
r = ¹/₂ × 12 cm
r = 6 cm
HITUNG LUAS BOLA (L)
L = 4πr²
= 4 × 3,14 × (6 cm)²
= 4 × 3,14 × 36 cm²
= 452,16 cm²
HITUNG VOLUME BOLA (V)
V = ⁴/₃ πr³
= ⁴/₃ × 3,14 × (6 cm)³
= ⁴/₃ × 3,14 × 216 cm³
= 904,32 cm³
d. Luas dan volume bola jika panjang jari jari (r) = 4,5 cm adalah 254,34 cm² dan 381,51 cm³.
Jawab :
HITUNG LUAS BOLA (L)
L = 4πr²
= 4 × 3,14 × (4,5 cm)²
= 4 × 3,14 × 20,25 cm²
= 254,34 cm²
HITUNG VOLUME BOLA (V)
V = ⁴/₃ πr³
Keterangan : V = volume bola (cm³)
π = ²²/₇ atau 3,14
r = jari jari bola (cm)
Penyelesaiannya :
V = ⁴/₃ πr³
= ⁴/₃ × 3,14 × (4,5 cm)³
= ⁴/₃ × 3,14 × 91,125 cm³
= 381,51 cm³
e. Luas dan volume bola jika diameter (d) = 20 m adalah 452,16 m² dan 904,32 m³.
Jawab :
HITUNG PANJANG JARI JARI (r)
r = ¹/₂ × d
Keterangan :
r = jari – jari bola
d = diameter bola
Penyelesaiannya :
r = ¹/₂ × d
r = ¹/₂ × 20 m
r = 10 m
HITUNG LUAS BOLA (L)
L = 4πr²
= 4 × 3,14 × (10 m)²
= 4 × 3,14 × 100 m²
= 1.256 m²
HITUNG VOLUME BOLA (V)
V = ⁴/₃ πr³
= ⁴/₃ × 3,14 × (10 m)³
= ⁴/₃ × 3,14 × 1.000 m³
= 4.186,67 m³
f. Luas dan volume bola jika panjang jari jari (r) = 15 m adalah 2.826 m² dan 14.130 m³.
Jawab :
HITUNG LUAS BOLA (L)
L = 4πr²
= 4 × 3,14 × (15 m)²
= 4 × 3,14 × 225 m²
= 2.826 m²
HITUNG VOLUME BOLA (V)
V = ⁴/₃ πr³
Keterangan : V = volume bola (cm³)
π = ²²/₇ atau 3,14
r = jari jari bola (cm)
Penyelesaiannya :
V = ⁴/₃ πr³
= ⁴/₃ × 3,14 × (15 m)³
= ⁴/₃ × 3,14 × 3.375 m³
= 14.130 m³
2. Penyelesaian soal a) diameter 8 cm
Karena diameter = 8 cm maka jari-jarinya = 4 cm, karena jari-jari setengah dari diameter
Luas belahan bola pepat (padat) = 3 x π x r²
= 3 x 3,14 x 4²
= 150,72 cm³
Penyelesaian soal b) jari-jari 12 cm
Luas belahan bola pepat (padat) = 3 x π x r²
= 3 x 3,14 x 12²
= 1.356,48 cm³
Penyelesaian soal c) diameter 12 cm
Karena diameter = 12 cm maka jari-jarinya = 6 cm, karena jari-jari setengah dari diameter.
Luas belahan bola pepat (padat) = 3 x π x r²
= 3 x 3,14 x 6²
= 339,12 cm³
Penyelesaian soal d) Jari-jari 8 m
Luas belahan bola pepat (padat) = 3 x π x r²
= 3 x 3,14 x 8²
= 602,88 m³
Penyelesaian soal e) Diameter 15 m
Karena diameter = 15 m maka jari-jarinya = 7,5 m, karena jari-jari setengah dari diameter.
Luas belahan bola pepat (padat) = 3 x π x r²
= 3 x 3,14 x 7,5²
= 529,875 m³
Penyelesaian soal f) Jari-jari 11 dm
Luas belahan bola pepat (padat) = 3 x π x r²
= 3 x 3,14 x 11²
= 1.139,82 m³
3. 1) Volume bola = ⁴/₃ x π x r³
2) Luas permukaan bola = 4 x π x r²
3) Luas belahan bola pepat (padat) = 3 x π x r²
Pembahasan
Luas setengah bola = ¹/₂ x Luas permukaan bola
= ¹/₂ x 4 x π x r²
= 2 x π x r²
Luas setengah bola tertutup = ¹/₂ x Luas permukaan bola + Luas lingkaran (tutup)
= ¹/₂ x 4 x π x r² + π x r²
= 2 x π x r² + π x r²
= 3 x π x r²
Setengah bola tertutup disebut juga bola pejal.
4.
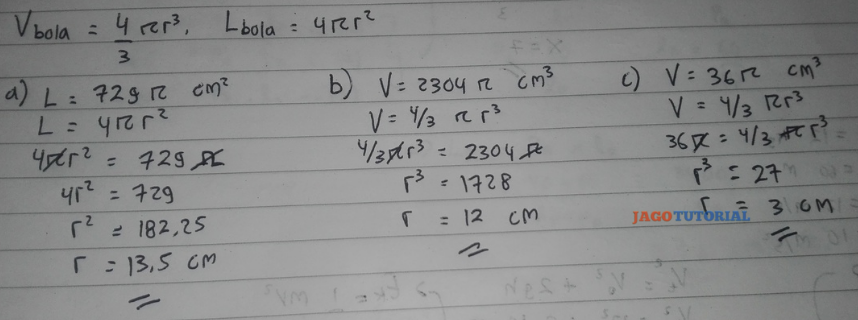
d. Diketahui : L = 27π m²
Ditanya : jari – jari (r) 1/2 bola tertutup ?
Jawab :
L = 3πr²
27π m² = 3πr²
r² = 27π m²/ 3π
r² = 9 m²
r = √9 m²
r = 3 m
∴ Kesimpulan jari-jari (r) setengah bola tertutup adalah 3 m.
e. Diketahui : L = 45π m²
Ditanya : jari – jari (r) 1/2 bola tertutup ?
Jawab :
L = 3πr²
45π m² = 3πr²
r² = 45π m²/ 3π
r² = 15 m²
r = √15 m²
r = 3,87 m
∴ Kesimpulan jari-jari (r) setengah bola tertutup adalah 3,87 m.
f. Diketahui : V = 128/3π m³
Ditanya : jari – jari (r) 1/2 bola tertutup ?
Jawab :
V = 2/3πr³
128/3π m³ = 2/3πr³
r³ = 128/3π m³ × 3/2π
r³ = 64 m³
r = ∛64 m³
r = 4 m
5. a. Luas permukaan = 4πr2 Volume = 4 3 πr3 4πr2 = 4 3 πr3 3 = r
b. Luas permukaan = 4πr2 = 4π(3)2 = 36π
6. Diket:
2 setengah bola terdiri dari 2 bola besar dan 1/2 bola kecil
r₁ = 4
r₂ = 8
Ditanya:
a.luas permukaan bangun tersebut
b.volume bangun tersebut.
Jawab:
a. Luas bola basar = 4πR²
= 4 x 3,14 (8)²
= 803,84 cm²
Luas bola kecil= 4πR²
= 4 x 3,14 (4)²
= 200,96 cm²
Luas setengah bola kecil= 1/2 : 200,96 = 100,48 cm²
Luas permukaan bangun = (luas bola besar)² + luas setengah bola kecil
= (803,84)² + 100,48
= 1708,16 cm²
b. Volume bola besar = (4/3)πR³
= 2143,6 cm³
Volume 2 bola besar= (4/3)πR³
= 4287,15 cm³
Volume bola kecil = (4/3)πR³
= 150,72 cm³
Volume setengah bola kecil= 75,36 cm³
Volume bangun= volume 2 bola besar + Volume setengah bola kecil
= 503,51 cm³
7. kesalahan yang dilakukan tergantung apakah bola tersebut bola padat (bola dengan isi) atau bola tanpa isi. luas permukaan setengah bola isi dengan kosong berbeda.
luas permukaan bola 4πr²
8. d = s
r = s/2
Lp = 4πr² = 4π x (s/2)² = 4πs²/4 = πs²
V = 4/3 πr³ = 4/3 π (s/2)³ = 4/3πs³/8 = πs³/6
9.

10. rumus volume bola adalah 4/3xπxr³ =perbedaannya hanya terdapat pada r nya yaitu 2 dan 4 jika dipangkat kan 3 menjadi 8 dan 64=1:8 jadi perbandingannya agar seimbang adalah tipe1:tipe2=8:1






