
- Tentukan jarak antara dua titik dari pasangan berikut
a. (10 , 20) dan (13 , 16)
b. (15 , 37) dan (42 , 73)
c. (-19 , -16) dan (-2 , 14)
Pembahasannya:
a. (10 , 20) dan (13 , 16)
x₁ = 10 dan y₁ = 20
x₂ = 13 dan y₂ = 16
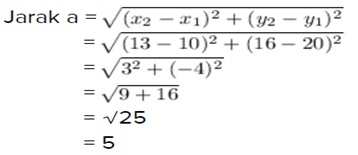
Jadi jarak pada titik (10 , 20) dan (13 , 16) adalah 5 satuan
b. (15 , 37) dan (42 , 73)
x₁ = 15 dan y₁ = 37
x₂ = 42 dan y₂ = 73
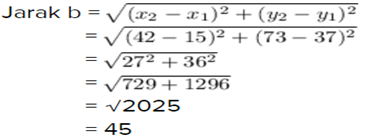
Jadi jarak pada titik (15 , 37) dan (42 , 73) adalah 45 satuan
c. (-19 , -16) dan (-2 , 14)
x₁ = -19 dan y₁ = -16
x₂ = -2 dan y₂ = 14
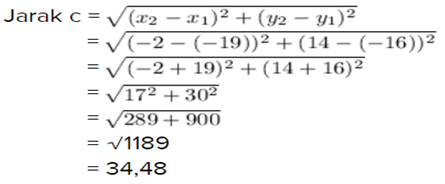
- Diketahui ∆ ABC dengan titik-titik A (-1 , 5), B (-1 , 1), dan C (2 , 1).
Apakah segitiga ABC merupakan segitiga siku-siku? Jelaskan.
Pembahasannya:
A (-1 , 5), dan B (-1 , 1)
x₁ = -1 dan y₁ = 5
x₂ = -1 dan y₂ = 1
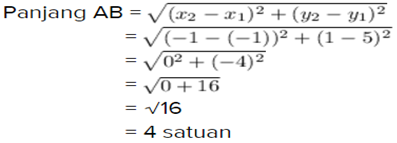
B (-1 , 1), dan C (2 , 1)
x₁ = -1 dan y₁ = 1
x₂ = 2 dan y₂ = 1
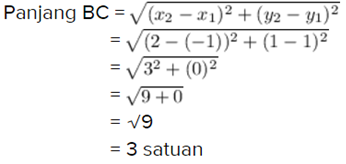
A (-1 , 5), dan C (2 , 1)
x₁ = -1 dan y₁ = 5
x₂ = 2 dan y₂ = 1
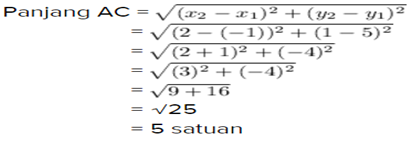
Bisa kita lihat pembuktiannya
AB² + BC² = AC²
4² + 3² = 5²
16 + 9 = 25
25 = 25
Jadi Δ ABC merupakan segitiga siku-siku, karena ketiga sisinya merupakan tripel pythagoras.
3. Tentukan luas daerah yang diarsir dari setiap gambar berikut
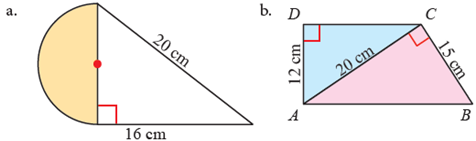
Pembahasannya:
a. tinggi segitiga sama dengan diameter setengah lingkaran (t = d)
misal : alas = a
tinggi = b
hipotenusa = c
Menentukan tinggi atau diameter
a² + b² = c²
16² + b² = 20²
256 + b² = 400
b² = 400 – 256
b² = 144
b = √144
b = 12
jadi diameter setengah lingkaran dan tinggi segitiga adalah 12 cm
jari-jari setengah lingkaran = 12/2 = 6 cm
L arsir 1/2 lingkaran
Luas = 1/2 π r²
= 1/2 × 3,14 × 6 × 6 cm²
= 3,14 × 18 cm²
= 56,52 cm²
Luas segitiga
L segitiga = 1/2 × a × t
= 1/2 × 16 × 12 cm²
= 96 cm²
Jadi luas yang diarsir setengah lingkaran adalah 56,52 cm²
b. Untuk Δ ABC
AB² = AC² + BC²
AB² = 20² + 15²
AB² = 400 + 225
AB² = 625
AB = √625
AB = 25 cm
L Δ ABC = 1/2 × AC × BC
= 1/2 ×20 × 15 cm²
= 150 cm²
Untuk Δ ACD
AC² = AD² + CD²
20² = 12² + CD²
400 = 144 + CD²
CD² = 400 – 144
CD² = 256
CD = √256
CD = 16 cm
L Δ ACD = 1/2 × AD × CD
= 1/2 × 12 × 16 cm²
= 96 cm²
L seluruh = L Δ ABC + L Δ ACD
= 150 cm² + 96 cm²
= 246 cm²
Jadi luas diarsir ABCD adalah 246 cm²
- Guru meminta kalian untuk menentukan jarak antara dua titik (4,2) dan (7,6). kamu menggunakan (4,2) sebagai (x1,y1) sedangkan temanmu menggunakan (7,6) sebagai (x1,y1). apakah kamu dan temanmu memperoleh hasil yang sama? Jelaskan
Pembahasannya:
Jarak dua titik , titik (4,2) dan titik (7,6)
Rumus pythagoras:
a = √{(y₂ – y₁)² + (x₂ – x₁)²}
Pada saat (4, 2) sebagai (x₁, y₁) adalah
a = √{(6 – 2)² + (7 – 4)²}
a = √(4² + 3²)
a = √(16+9)
a = √25
a = 5
Pada saat (7, 6) sebagai (x₁, y₁) adalah
a = √{(y₂ – y₁)² + (x₂ – x₁)²}
a = √{(2 – 6)² + (4 – 7)²}
a = √{(-4)² + (-3)²}
a = √(16+9)
a = √25
a = 5
Ternyata hasilnya sama, karena bilangan negatif bila dikuadratkan hasilnya positif, sehingga dibolak-balik angkanya meskipun yang pertama hasilnya positif dan yg kedua hasilnya negatif tetap sama
- Ahmad dan Udin berdiri saling membelakangi untuk main tembak-tembakan pistol bambu. Ahmad berjalan 20 langkah ke depan kemudian 15 langkah ke kanan. Pada saat yang sama, Udin berjalan 16 langkah ke depan kemudian 12 langkah ke kanan. Udin berhenti kemudian menembak Ahmad.
a. Gambar situasi di atas dengan menggunakan bidang kartesius.
b. Berapa langkah jarak mereka berdua saat Udin menembak Ahmad dengan pistol bambu?
Pembahasannya:
a. Gambar situasi menggunakan bidang kartesius.
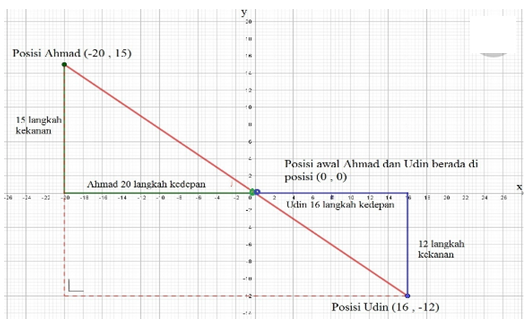
b. Jarak langkah mereka berdua saat Udin menembak Ahmad bisa menggunakan dua cara.
- Menghitung petak langkah dengan menggunakan pythagoras
c² = a² + b²
AU² = (20 + 16)² + (15 + 12)2
AU² = 36² + 27²
AU² = 1296 + 729
AU² = 2025
AU = √2025
AU = 45 satuan langkah
Jadi jarak mereka berdua saat Udin menembak Ahmad dengan pistol bambu adalh 45 langkah.
2. Menghitung jarak dua titik antara Ahmad dan Udin yaitu (-20 , 15) dan (16 , -12)
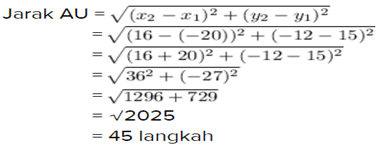
Jadi jarak mereka berdua saat Udin menembak Ahmad dengan pistol bambu adalh 45 langkah.
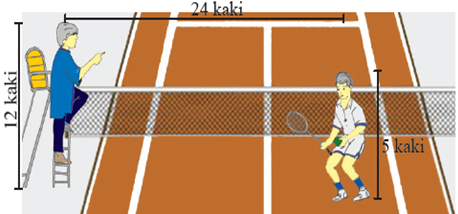
- Seorang atlet tenis mengajukkan pertanyaan kepada wasit. Suara atlet mampu didengar wasit hanya pada jarak maksimum 30 kaki. Berdasarkan posisi wasit dan atlet tenis pada gambar berikut,
dapatkah wasit mendengar suara sang atlet? Jelaskan jawaban kalian.
Pembahasan:
Diketahui :
jarak antara wasit dan atlet = 24 kaki
ketinggian wasit melihat = 12 kaki
tinggi atlet = 5 kaki
Ditanyakan :
dapatkah wasit mendengar suara sang atlet, jika jarak maksimum pendengaran 30 kaki?
Jawab:
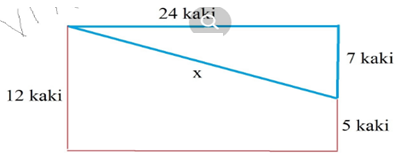
Untuk menghitung jarak pendengaran kita bisa gunakan pythagoras
c² = a² + b²
x² = 24² + (12 – 5)²
x² = 24² + 7²
x² = 576 + 49
x² = 625
x = √625
x = 25 kaki
Jadi jarak pendengaran wasit dan atlet adalah 25 kaki, maka suara wasit dapat terdengar karena < 30 kaki.
- Tinggi sebuah jendela lantai 2 pada sebuah gedung kira-kira 8 meter .
Di depan gedung tersebut ada sebuah taman dengan lebar 6 meter.
Berapa panjang tangga minimum yang dibutuhkan agar kaki-kaki
tangga tidak merusak taman tersebut ?
Pembahasannya:
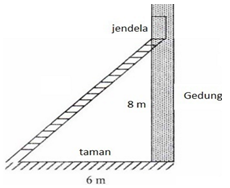
Diketahui
Tinggi jendela lantai 2 = a = 8 meter
Lebar taman = b = 6 meter
Ditanyakan
Panjang tangga minimum yang dibutuhkan agar kaki-kaki tangga
tidak merusak taman tersebut c = …?
Jawab
Dengan menggunakan teorema pythagoras, diperoleh
c² = a² + b²
c² = 8² + 6²
c² = 64 + 36
c² = 100
c = √(100)
c = 10
Jadi panjang tangga minimum yang dibutuhkan agar kaki-kaki tangga
tidak merusak taman tersebut adalah 10 meter
- Seorang penyelam dari tim sar mengaitkan dirinya pada tali sepanjang 25 m untuk mencari sisa-sisa bangkai pesawat di dasar laut. Laut diselami memiliki kedalaman 20 meter dan dasarnya rata.
Berapa luas derah yang mampu dijangkau oleh penyelam tersebut?
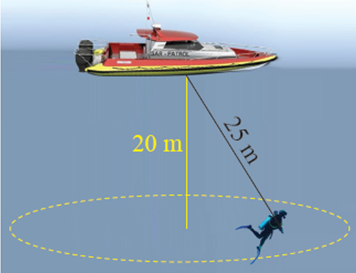
Pembahasannya:
Mencari panjang Jari-Jari (r) = Sisi Alas Δ:
Sisi Miring = 25 m
Sisi Tegak = 20 m

Luas Daerah = Luas Lingkaran adalah
π = 3,14
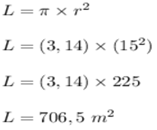
Jadi daerah dasar laut yang dapat dijangkau oleh penyelam adalah seluas 706,5 m².
9. Tentukan panjang AG dari bangun berikut?
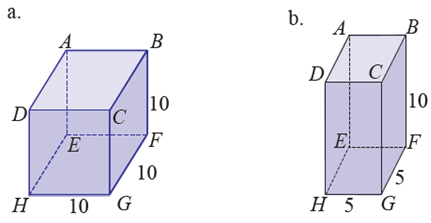
Pembahasan:
a. Pada kubus ABCD.EFGH
AG² = s² + s² + s²
AG² = HG² + FG² + BF²
AG² = 10² + 10² + 10²
AG² = 10² × 3
AG = √(100 × 3)
AG = 10√3
Jadi panjang AG pada kubus adalah 10√3
b. Pada balok ABCD.EFGH
AG² = p² + l² + t²
AG² = HG² + FG² + BF²
AG² = 5² + 5² + 10²
AG² = 25 + 25 + 100
AG² = 150
AG = √150
AG = √(25 x 6)
AG = 5√6
Jadi panjang AG pada balok adalah 5√6
- Bola A dan bola B digantung pada suatu kawat lurus seperti pada gambar di bawah. Diameter Bola A dan bola B berturut-turut adalah 8 dan 18. Jika jarak ujung tali l dan n pada kawat adalah 5 dan panjang tali l adalah10, berapakah panjang minimum tali n agar kedua tali bisa sejajar dan bola tidak saling menekan?
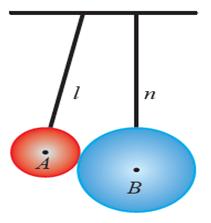
Pembahasaanya:
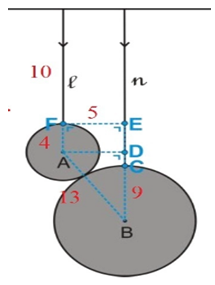
Dari perpanjangan tali n, sehingga terbentuk persegi panjang ADEF dan segitiga ABD
Diketahui :
panjang tali l = 10 cm
AF = DE = ¹/₂ × 8 = 4 cm
BC = ¹/₂ × 18 = 9 cm
AB = AF + BC = 4 + 9 = 13 cm
EF = AD = 5 cm
Ditanyakan :
panjang minimum tali n agar kedua tali bisa sejajar dan bola tidak saling menekan ?
Jawab :
Perhatikan segitiga siku-siku ADB :
AB² = AD² + BD²
13² = 5² + BD²
169 = 25 + BD²
BD² = 169 – 25
BD² = 144
BD = √144
BD = 12 cm
CD = BD – BC
CD = 12 – 9
CD = 3 cm
Panjang tali n = panjang tali l + DE + CD
= 10 cm + 4 cm + 3 cm
= 17 cm
Jadi panjang minimum tali n agar kedua tali bisa sejajar dan bola tidak saling menekan adalah 17 cm







