Latihan 5.2 Kerucut Semester 2
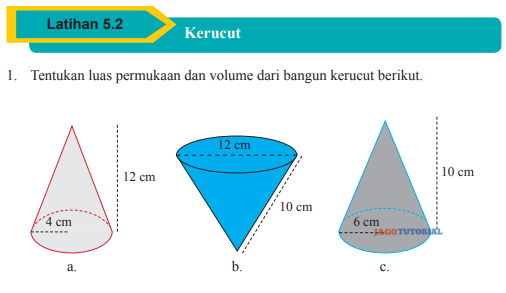
1. Tentukan luas permukaan dan volume dari bangun kerucut berikut.
2. Tentukan panjang dari unsur kerucut yang ditanyakan.
3. Tumpeng. Pada suatu hari Pak Budi melakukan 8 cm syukuran rumah baru. Pak Budi memesan suatu tumpeng. Tumpeng tersebut memiliki diameter 36 cm dan tinggi 24 cm. Namun, diawal acara Pak Budi memotong bagian atas tumpeng tersebut secara mendatar setinggi 8 cm. Berapakah luas permukaan dan volume dari tumpeng yang tersisa?
4. Suatu kerucut memiliki jari-jari 6 cm dan tinggi t cm. Jika luas permukaan kerucut adalah A cm2 dan volume kerucut adalah A cm3 maka tentukan: a. Nilai dari t. b. Nilai dari A.
5. Terdapat suatu bangun ruang yang diperoleh dari dua kerucut yang sepusat kerucut yang lebih besar memiliki jari-jari 10 cm dan tinggi 24 cm jari-jari kerucut kecil adalah setengah jari-jari kerucut besar tinggi kerucut kecil setengah dari tinggi kerucut besar Tentukan luas permukaan yang gelap
6. irisan kerucut. misalkan terdapat suatu kerucut dengan jari-jari r cm dan panjang t cm. kemudian kerucut tersebut dijadikan irisan kerucut dengan memotong kerucut tersebut menjadi dua bagian dari atas ke bawah ( lihat gambar di atas ). tentukan rumus untuk menghitung luas irisan kerucut tersebut.
7. Analisis kesalahan. Budi menghitung volume kerucut dengan diameter 10 cm dan tinggi 12 cm. Budi menghitung
V=⅓ (12)² (10) = 480
sehingga diperoleh volume adalah 480 cm³. tentukan kesalahan yang dilakukan Budi
8. dari kertas karton ukuran 1 m × 1 m Lisa akan membuat jaring jaring kerucut dengan jari jari r cm dan tinggi t cm. a.Apakah Lisa bisa membuat jaring jaring tersebut jika r = 40 cm dan t = 30 cm? Kemukakan alasanmu. b.Apakah Lisa membuat jarinfg jaring tersebut jika r = 30 cm dan t = 40 cm? Kemukakan alasanmu.
9. Kerucut miring. Pada gambar di bawah terdapat dua buah bangun sisi lengkung. Gambar sebelah kiri merupakan kerucut dengan jari-jari r dan tinggi t. Gambar sebelah kanan merupakan bangun ruang sisi lengkung yang diperoleh dari kerucut sebelah kiri dengan menggeser alasnya ke sebelah kanan, selanjutnya disebut dengan kerucut miring. Kerucut miring tersebut memiliki jari-jari r dan tinggi t.
a. Tentukan suatu metode untuk mendapatkan rumus dari volume kerucut miring tersebut.
b. Apakah volume rumus kerucut miring sama dengan volume kerucut? Jelaskan analisismu.
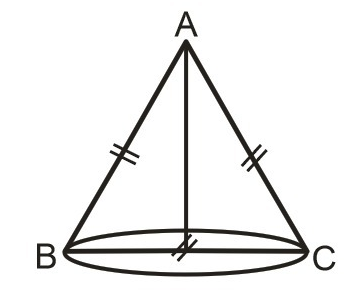
10. Perhatikan kerucut di samping. Jika segitiga ABC merupakan segitiga sama sisi dengan panjang sisi d cm, tentukan luas permukaan dan volume kerucut.
Kunci Jawaban Latihan 5.2 Kerucut Halaman 293 Semester 2
1. a. Garis pelukis² = alas² + tinggi²
Garis pelukis² = ( 4 cm )² + ( 12 cm )²
Garis pelukis² = 16 cm² + 144 cm²
Garis pelukis = √ ( 160 cm² )
Garis pelukis = 12.65 cm
Luas permukaan kerucut = π x r (r + s)
Luas permukaan kerucut = 3.14 x 4 cm (4 cm + 12.65 cm)
Luas permukaan kerucut = 3.14 x 4 cm ( 16.25 cm )
Luas permukaan kerucut = 204.1 cm²
Volume = ¹/₃ x π r² x t
Volume = ¹/₃ x 3.14 x ( 4 cm )² x 12 cm
Volume = ¹/₃ x 3.14 x 16 cm² x 12 cm
Volume = 200.96 cm³
b. Garis pelukis² = alas² + tinggi²
( 10 cm )² = ( 6 cm )² + tinggi ²
100 cm² = 36 cm² + tinggi²
tinggi² = 100 cm² – 36 cm²
tinggi = √ ( 64 cm² )
tinggi = 8 cm
Luas permukaan kerucut = π x r (r + s)
Luas permukaan kerucut = 3.14 x 6 cm (6 cm + 10 cm)
Luas permukaan kerucut = 3.14 x 6 cm ( 16 cm )
Luas permukaan kerucut = 301.44 cm²
Volume = ¹/₃ x π r² x t
Volume = ¹/₃ x 3.14 x ( 6 cm )² x 8 cm
Volume = ¹/₃ x 3.14 x 36 cm² x 8 cm
Volume = 301.44 cm²
c. *volume kerucut
= 1/3 x π x r^2 x t
*luas permukaan kerucut
= πr(r + s)
r = 6
s = 10
s^2 = r^2 + t^2
10^2 = 6^2 + t^2
100 = 36 + t^2
t = √64
t = 8
volume kerucut
V = 1/3 x π x r^2 x t
V = 1/3 x 3,14 x 6^2 x 8
V = 1/3 x 3,14 x 36 x 8
V = 96 x 3,14
V = 301,44
V = 376,8
luas permukaan kerucut
= πr(r + s)
= 3,14 x 6(6 + 8)
= 18,84(14)
= 263,76
d. t = √25²-7² = 24 cm
Lp = 22/7 x 7 x (7+25) = 22 x 32 = 704 cm²
V = 22/7 x 7² x 24/3 = 154 x 8 = 1.232 cm³
e. Garis pelukis² = alas² + tinggi²
( 4 cm )² = alas² + ( 3 cm )²
16 cm² = alas² + 9 cm²
alas² = 16 cm² – 9 cm²
alas = √ ( 7 cm² )
alas = 2.65 cm
Luas permukaan kerucut = π x r (r + s)
Luas permukaan kerucut = 3.14 x 2.65 cm (2.65 cm + 4 cm)
Luas permukaan kerucut = 3.14 x 2.65 cm ( 6.65 cm )
Luas permukaan kerucut = 55.33 cm²
Volume = ¹/₃ x π r² x t
Volume = ¹/₃ x 3.14 x ( 2.65 cm )² x 3 cm
Volume = ¹/₃ x 3.14 x 7 cm² x 3 cm
Volume = 21.98 cm³
f. Garis pelukis² = alas² + tinggi²
( 13 cm )² = ( 5 cm )² + tinggi ²
169 cm² = 25 cm² + tinggi²
tinggi² = 169 cm² – 25 cm²
tinggi = √ ( 144 cm² )
tinggi = 12 cm
Luas permukaan kerucut = π x r (r + s)
Luas permukaan kerucut = 3.14 x 5 cm (5 cm + 13 cm)
Luas permukaan kerucut = 3.14 x 5 cm ( 18 cm )
Luas permukaan kerucut = 282.6 cm²
Volume = ¹/₃ x π r² x t
Volume = ¹/₃ x 3.14 x ( 5 cm )² x 12 cm
Volume = ¹/₃ x 3.14 x 25 cm² x 12 cm
Volume = 314 cm²
2. a.Volume=300 pi m pangkat 3
Jari-jari = 10m
t = 3V/πr² = (3 x 300π) / (π x 10²) = 900π/100π = 9 m
b.volume = 120 pi m pangkat 2
t = 10m
r = √(3×120π)/(10π) = √(360π/10π) = √36 = 6 m

3.

4.

5. kerucut 1: s=26
luas permukaan= 3,14 x 100 +3,14 x 10 x 26 = 314+816,4 = 1130,4
volum= 1/3 x 3,14 x 10 x 10 x 24=2512
kerucut 2: r=5, t=12, s=13
luas permukaan=3,14 x 25 + 3,14 x 5 x 13=78,5 + 204,1=282,6
volum=1/3 x 3,14 x 5 x 5 x 12 = 314
6. irisannya berbentuk segi tiga
jadi rumusnya
= 1/2 × alas × tinggi
= 1/2 × (2 × jari-jari) × tinghi
= 1/2 × 2r × t
= r × t
7. Budi salah mensubstitusikan nilai r dan t, selain itu jari-jarinya adalah 10/2 = 5
8. – Luas permukaan kerucut a
s₁ = √(30²+40²)
s₁ = √(900+1600)
s₁ = √2500
s₁ = 50 cm
L kerucut a
= π r₁² + π r₁ s₁
= 3,14×40×40 + 3,14×40×50
= 3768 + 6280
= 10048 cm²
Luas permukaan kerucut b
s₂ = √(40²+30²)
s₂ = √(1600+900)
s₂ = √2500
s₂ = 50
L kerucut b
= π r₂² + π r₂ s₂
= 3,14×30×30 + 3,14×30×50
= 2826 + 4710
= 7536 cm²
– Luas kertas karton Lisa
= 1 m × 1 m
= 100 cm × 100 cm
= 10000 cm²
** Luas karton yang diperlukan Lisa untuk jaring-jaring a LEBIH BESAR daripada karton yang dimiliki Lisa.
L kerucut a > L karton
10048 cm² > 10000 cm²
Maka, Lisa TIDAK BISA membuat jaring-jaring kerucut a dengan karton yang dimilikinya.
** Luas karton yang diperlukan Lisa untuk jaring-jaring b LEBIH KECIL daripada karton yang dimiliki Lisa.
L kerucut b < L karton
7536 cm² < 10000 cm²
Maka, Lisa BISA membuat jaring-jaring kerucut b dengan karton yang dimilikinya.
Lisa BISA membuat jaring-jaring kerucut dari kertas karton yang dimilikinya jika jari-jari kerucut 30 cm dan tinggi kerucut 40 cm. Lisa TIDAK bisa membuat jaring-jaring kerucut dari kertas karton yang dimilikinya jika jari-jari kerucut 40 cm dan tinggi kerucut 30 cm.
9. a. Salah satu metodenya adalah dengan membuat tumpukan koin yang membentuk kerucut miring.
b. Sama, karena kaidah volume adalah luas alas dikalikan dengan tinggi. Dengan mengubah kerucut menjadi kerucut miring tidak mengubah alas dan tingginya, sehingga tidak terjadi perubahan volume.
10. Jika segitiga ABC merupakan segitiga sama sisi dengan panjang sisi d cm, Luas permukaan dan volume kerucut berturut-turut adalah 3/4 d² π cm² dan √3 / 24 d³π cm³
Volume Kerucut = 1/3 · π · r² · t
Luas Permukaan Kerucut = π·r² + π·r·s = π·r · (r + s)
AB = BC = AC = d cm
AB dan AC adalah Garis pelukis kerucut (s).
BC adalah diameter (d) kerucut, sehingga jari-jari kerucut (r) = 1/2 BC = 1/2 d