
Ayo Kita Berlatih 7.4 Semester 2
Bagian A
1. Sudut yang terbentuk antara diameter dengan garis singgung lingkaran adalah ….
2. Diketahui jarak antara pusat lingkaran A dan B adalah 20 cm. Lingkaran A dan B memiliki jari-jari berturut-turut 22 cm dan 6 cm. Panjang garis singgung persekutuan luarnya adalah … cm.
3. Pada gambar di samping, suatu busur dibuat dengan pusat P dan memotong garis di titik Q. Kemudian dengan jarijari yang sama, dibuat busur dengan pusat Q, sedemikian hingga memotong busur pertama di titik R. Dari titik P, Q, dan R, dibuat sudut PRQ. Ukuran sudut yang terbentuk dari sudut PRQ adalah ….
4. Pada gambar berikut, ABCD adalah suatu persegi panjang. Lingkaran P dan Q adalah lingkaran yang sisi-sisinya saling bersinggungan dengan sisi persegi panjang.
Jika jari-jari masing-masing lingkaran tersebut adalah 5 cm, maka luas persegi panjang adalah ….
5. Diketahui dua lingkaran berbeda. Jari-jari lingkaran pertama adalah 15 cm, sedangkan jari-jari lingkaran kedua adalah 8 cm. Jika jarak pusat kedua lingkaran tersebut adalah 25 cm, maka panjang garis singgung persekutuan luar kedua lingkaran tersebut adalah … cm
Bagian B
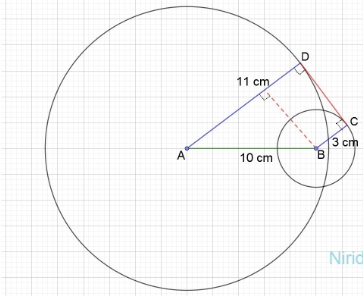
1. Diketahui jarak antara pusat lingkaran A dan B adalah 10 cm. Lingkaran A dan B memiliki jari-jari berturut-turut 11 cm dan 3 cm. Tentukan: a. panjang garis singggung persekutuan luarnya (jika ada); b. sketsa gambarnya (lengkap dengan garis singgung persekutuan luarnya, jika ada).
2. Diketahui panjang garis singgung persekutuan luar lingkaran C dan D adalah 24 cm. Jari-jari lingkaran C dan D berturut-turut 15 cm dan 8 cm. Tentukan:
a. jarak pusat kedua lingkaran tersebut (jika ada);
b. jarak kedua lingkaran tersebut (jika ada).
3. Diketahui jarak antara lingkaran E dan F adalah 5 cm. Lingkaran E dan F memiliki jari-jari berturut-turut 13 cm dan 4 cm. Tentukan panjang garis singgung persekutuan luar kedua lingkaran tersebut. (jika ada)
4. Diketahui jumlah diameter lingkaran G dan H adalah 30 cm. Panjang garis singgung persekutuan luarnya adalah 24 cm. Sedangkan jarak kedua pusat lingkaran tersebut adalah 26 cm. Tentukan:
a. jari-jari kedua lingkaran tersebut,
b. jarak kedua lingkaran.
5. Diketahui jarak pusat lingkaran I dan J adalah 12 cm. Lingkaran I memiliki jari-jari 8 cm. Tentukan jari-jari J maksimal agar terdapat garis singgung persekutuan luar antara lingkaran I dan J. Jelaskan alasanmu.
Kunci Jawaban Ayo Kita Berlatih 7.4 Halaman 102 Semester 2
Bagian A
1. B. siku-siku
2. P = 20 cm
R = 22 cm
r = 6 cm
L=…
P²= L²+(R-r)²
20²=L²+(22-6)²
20²=L²+16²
400=L²+256
L²=400-256
L²=144
L=√144
L=12
b. 12 cm
3. c. 60 derajat
4. jari-jari (r) = 5 cm
dua lingkaran
Panjang AB = 4 × r
= 4 × 5 cm
= 20 cm
Panjang AD = 2 × r
= 2 × 5 cm
= 10 cm
Luas persegi panjang ABCD = AB × AD
= 20 cm × 10 cm
= 200 cm²
Jadi luas persegi panjang ABCD adalah 200 cm² (D)
5. Panjang garis singgung
= √(jarak pusat² – (R – r)²)
= √(25² – (15 – 8)²)
= √625 – 49)
= √576
= 24 cm
Bagian B
1. a. panjang garis singgung persekutuan luar
garis singgung persekutuan luar kita beri nama CD
CD² = AB² – (AD – BC)²
= 10² – (11 – 3)²
= 10² – 8²
= 100 – 64
= 36
CD = √36
= 6 cm
Jadi panjang garis singgung persekutuan luar adalah 6 cm
b.
2. p² = L² + (R-r)²
dengan:
p = jarak kedua pusat lingkaran
L = panjang garis singgung persekutuan luar
R = panjang jari-jari lingkaran besar
r = panjang jari-jari lingkaran kecil
a) L= 24 cm
R = 15 cm
r = 8 cm
p² = L² + (R-r)²
p² = 24² +(15-8)²
p² = 576 + 7²
p² = 576 + 49
p² = 625
p = √ 625
p = 25
Jadi, jarak pusat kedua lingkaran tersebut adalah 25 cm
b) jarak kedua lingkaran tersebut
= jarak pusat kedua lingkaran – (panjang jari-jari lingkaran besar + panjang jari-jari lingkaran kecil)
= p – (R+r)
= 25 cm – (15 cm + 8 cm)
= 25 cm – 23 cm
= 2 cm
Jadi, jarak kedua lingkaran tersebut adalah 2 cm.
3. Jarak kedua O (s) = 5 cm
Jari² O E (RE) = 13 cm
Jari² O F (RF) = 4 cm
Hitung dulu jarak antara Kedua pusat (p) dengan menjumlahkan Kedua jari² dan nilai s.
P = s + RE + RF
P = 5 + 13 + 4
P = 22
Rumus umum garis singgung PerLu =
D = √(p^2 – (r1 – r2)^2)
Penghitungan
D = √(p^2 – (RE – RF)^2)
D = √(22^2 – (13 – 4)^2)
D = √(484 – (9)^2)
D = √(484 – 81)
D = √403
D = 20,1
4. Diketahui :
d₁ + d₂ = 30 cm
garis singgung persekutuan luar (d) = 24 cm
jarak pusat kedua lingkaran (p) = 26 cm

576 = 676 – (R – r)²
(R – r)² = 676 – 576
(R – r)² = 100
R – r = √100
R – r = 10 … pers II
a. menentukan panjang jari-jari kedua lingkaran
eliminasi pers I dan II
R + r = 15
R – r = 10
————- +
2R = 25
R = 25/2
R = 12,5 cm
subtitusi
R + r = 15
12,5 + r = 15
r = 15 – 12,5
r = 2,5 cm
Jadi jari-jari kedua lingkara tersebut adalah 12,5 cm dan 2,5 cm
b. KL = p – (R + r)
= 26 cm – (12,5 + 2,5) cm
= 26 cm – 15 cm
= 11 cm
5. Diketahui :
Jarak pusat (p) = 30 cm
jari-jari (I) = 8 cm
Ditanya :
Jari-jari J maksimal ?
Jawab :
Untuk jari-jari maksimal agar terdapat garis persekutuan dalam dan mempunyai jarak pusat 30 cm, maka kedua lingkaran saling bersinggungan atau saling berimpit
Jadi garis singgung persekutuan dalamnya pas ditengah pada kedua lingkaran saling bersentuhan yang berupa garis merah pada gambar.
Maka jari-jari maksimalnya adalah jarak antar pusat dikurang dengan jari-jari I
Jari-jari J maksimal = p – I
= 30 cm – 8 cm
= 22 cm
Jadi panjang jari-jari J maksimal adalah 22 cm






