Latihan 4.1 Kekongruenan Bangun Datar Semester 2
1. Manakah di antara gambar di bawah ini yang kongruen?
2. Manakah di antara gambar di bawah ini yang kongruen?
3. Apakah menurutmu pensil warna pada gambar di samping ini kongruen? Jelaskan.
4. Tuliskan pasangan bangun yang kongruen. Tuliskan langkahmu menentukan bangun tersebut, digeser (translasi), diputar (rotasi), atau gabungannya?
5. Berikut ini adalah pasangan bangun yang kongruen. Tuliskan sisi-sisi dan sudutsudut yang bersesuaian
6. Manakah belah ketupat di bawah ini yang kongruen? Jelaskan.
7. Diketahui trapesium ABCD dan trapesium FEHG adalah kongruen. Jika panjang sisi AD = 12 cm, DC = 13 cm dan EF = 22 cm maka tentukan panjang EH.
8. Jika dua gambar di samping kongruen, tentukan nilai u dan v pada gambar tersebut.
9. Perhatikan dua gambar rumah tampak dari depan yang kongruen berikut ini.
a. Tentukan sisi-sisi yang bersesuaian.
b. Tentukan sudut-sudut yang bersesuaian.
c. Berapa panjang KJ, KL, dan LM?
d. Berapa keliling dan luas JKLMN jika jarak J ke LM adalah 7 m?
10. Analisis kesalahan Jelaskan dan perbaikilah pernyataan salah berikut
“Kedua bangun di samping mempunyai empat sisi dan sisi sisi yang bersesuaian sama panjang.Jadi kedua bangun tersebut kongruen”
11. Trapesium pd gambar disamping ini kongruen. tentukan pertanyaan berikut ini benar atau salah. jelaskan.Besar <Z= 140°
Besar <C= 40°
sisi WZ bersesuaian dengan sisi CB
keliling bangun ABCD= keliling WXYZ. Luas bangun ABCD tidak sama dngn luas WXYZ
12. Gambar disamping menunjukan dua cara menggambar satu garis untuk membagi persegi panjang menjadi dua bangun yang kongruen.gambarkan tiga cara lainya
13. Apakah luas dua bangun yang kongruen pasti sama?
apakah dua bangun dengan luas yang sama pasti kongruen ?
jelaskan dengan gambar/diagram untuk mendukung jawabanmu.
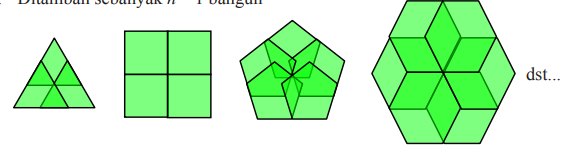
14. Berpikir Kritis Berapa banyak segitiga sama sisi kongruen paling sedikit yang diperlukan untuk membentuk segitiga samasisi yang ukurannya lebih besar dari segitiga sama sisi semula? Demikian juga, berapa persegi kongruen paling sedikit yang diperlukan untuk menghasilkan persegi yang ukurannya lebih besar dari persegi semula? Dapatkah hasil ini diperluas untuk segi-n beraturan yang lain? Jelaskan alasanmu. Harus ditambah berapa banyak segi-n beraturan lagi supaya tetap jadi segi-n?
Kunci Jawaban Latihan 4.1 Kekongruenan Bangun Datar Halaman 212 Semester 2
1. a – j, b – i, c – f, d – g, e – h
2. a – d – h, b – e – i, c – f – g
3. Jika pensil warna tersebut baru dibeli (belum dipakai sama sekali), maka pensil-pensil warna tersebut kongruen karena ukuran dan bentuknya sama persis. Perbedaan warna tidak mempengaruhi kekongruenan.
Tetapi jika pensil tersebut sudah dipakai beberapa, maka pensil warna tersebut sudah tidak kongruen lagi karena ukurannya jadi berbeda dari sebelumnya.
4. A – D – M, I – L, dan C – O
5. i. sisi-sisi yang bersesuaian adalah:
AB = NO
BC = OM
AC = NM
Sudut-sudut yang bersesuaian adalah:
∠ABC = ∠NOM
∠BAC = ∠ONM
∠BCA = ∠OMN
ii. sisi-sisi yang bersesuaian adalah:
AB = NO
BC = MN
CD = MP
DA = PO
Sudut-sudut yang bersesuaian adalah:
∠ABC = ∠ONM
∠BCD = ∠NMP
∠CDA = ∠MPO
∠DAB = ∠PON
iii. sisi-sisi yang bersesuaian adalah:
AB = DE
BC = EF
AC = DF
Sudut-sudut yang bersesuaian adalah:
∠ABC = ∠DEF
∠BAC = ∠EDF
∠BCA = ∠EFD
pada gambar (iv) bangun ABCD kongruen dengan bangun JKLM, maka : sisi-sisi yang bersesuaian, yaitu: AB = JK, BC = KL, CD = LM, DA = MJ ; sementara sudut-sudut yang bersesuaian, yaitu : ∠ABC = ∠JKL, ∠BCD = ∠KLM, ∠CDA = LMJ, ∠DAB = ∠MJK
pada gambar (v) bangun JKLMN kongruen dengan bangun QRSTU, maka : sisi-sisi yang bersesuaian, yaitu: JK = RS, KL = QR, LM = UQ, MN = TU, NJ = ST ; sementara sudut-sudut yang bersesuaian, yaitu : ∠JKL = ∠QRS, ∠KLM = ∠RQU, ∠LMN = TUQ, ∠MNJ = ∠STU, ∠NJK = ∠RST
pada gambar (vi) bangun PQRST kongruen dengan bangun VWXYZ, maka : sisi-sisi yang bersesuaian, yaitu: PQ = VW, QR = VZ, RS = YZ, ST = XY, TP = WX ; sementara sudut-sudut yang bersesuaian, yaitu : ∠PQR = ∠WVZ, ∠QRS = ∠VZY, ∠RST = ∠XYZ, ∠STP = ∠WXY, ∠TPQ = ∠VWX
bangun a dan c memiliki ukuran panjang yang sama , namun belum tentu kongruen jika ukuran sudutnya tidak sama , sekarang kita lihat dan kita hitung ukuran sudutnya
6. Pada gambar a , ukuran panjang 5 cm , ukuran sudut yang ada 50 derajat ,kita cari ukuran sudut yang lain , ukuran sudut yang lain = 180 – 50 = 130 derajat
pada gambar c , ukuran panjang 5 cm , ukuran sudut yang ada 130 derajat , kita cari ukuran sudut yang lain , ukuran sudut yang lain = 180 – 130 = 50 derajat
sekarang dapat kita simpulkan bahwa gambar a dan gambar c kongruen karena baik ukuran panjang maupun ukuran sudut dan bentuk bangun sama
7. AB = EF = 22 cm
ambil titik diantara AB dan tega lurus dengan C kita misalkan titik Z, maka
AZ = DC = 13 cm
CZ = AD = 12 cm
BZ = AB – AZ = 22 cm – 13 cm = 9 cm
CB² = CZ² + BZ²
= 12² + 9²
= 144 + 81
CB² = 225
∴ CB = √225 = 15 cm
karna ABCD dan EFGH adalah kongruen, maka
CB = EH = 15 cm
Jadi panjang EH adalah 15 cm
8. Bangun ABCD
∠A = 80ᵒ, ∠B = 135ᵒ, ∠C = 75ᵒ maka
∠D = 360ᵒ – (80ᵒ + 135ᵒ + 75ᵒ)
∠D = 360ᵒ – 290ᵒ
∠D = 70ᵒ
Bangun PQRS
∠S = 135ᵒ, ∠P = u dan ∠Q = v
AB = SR (ada tanda garis dua)
BC = PS (ada tanda garis satu)
Karena ABCD kongruen dengan PQRS, maka sudut-sudut yang bersesuaiannya sama besar
AB = SR dengan ∠A = 80ᵒ, ∠B = 135ᵒ dan ∠S = 135ᵒ, maka otomatis ∠R = 80ᵒ
BC = PS dengan ∠B = 135ᵒ, ∠C = 75ᵒ dan ∠S = 135ᵒ, ∠P = u maka otomatis u = 75ᵒ
Jadi
∠A = ∠R = 80ᵒ
∠B = ∠S = 135ᵒ
∠C = ∠P = 75ᵒ ⇒ u = 75ᵒ
Sehingga
∠D = ∠Q = 70ᵒ ⇒ v = 70ᵒ
9. a. AE = JN
ED = NM
DC = ML
CB = LK
AB = JK
b. ∠A = ∠J, ∠E = ∠N, ∠B = ∠K, ∠C = ∠L, ∠D = ∠M
c. JK = AB = 5 m, KL = BC = 4 m, LM = CD = 8 cm
d. K = JN + NM + ML + LK + KJ
= 5 + 4 + 8 + 4 + 5
= 26 m
L = luas segitiga JNK + luas persegi panjang KLMN
= 12 m² + 32 m²
= 44 m²
10. Dari definisi tersebut, dengan mudah kita bisa mengetahui kesalahan dari pernyataan di atas, yaitu
segi empat dengan sisi-sisi bersesuaian sama panjang belum tentu kongruen, karena bisa jadi sudut-sudut yang bersesuaian tidak sama besar.
Salah satu pernyataan benar yang bisa digunakan untuk memperbaiki pernyataan di atas adalah:
“ Kedua bangun di samping mempunyai empat sisi dengan sisi-sisi yang bersesuaian sama panjang, serta memiliki empat sudut dengan sudut-sudut bersesuaian sama besar. Jadi, kedua bangun tersebut kongruen.”
11. Pembuktian trapesium ABCD dan WXYX kongruen
sisi-sisi yg sama panjang
AB = YZ
AD = XY
CD = WX
BC = WZ
Karena ada pernyataan Keliling bangun ABCD sama dengan keliling WXYZ.
sudut-sudut yg sama besar
∠ BAD = ∠ XYZ = 90°
∠ ADC = ∠ WXY = 90°
∠ BCD = ∠ XWZ = 40°
∠ ABC = ∠ WZY = 140°
Jadi kedua trapesium ABCD dan WXYZ adalah kongruen
12.

13. jawaban soal 1
ya , karna kkongruen memilii sisi yg sama panjang
jawaban soal 2
tidak , karena bangun tersebut belum tentu sisi-sisnya sama panjang
14. Untuk membentuk bangun konruen yg lebih besar, maka segitiga sama sisi dan persegi membutuhkan setidaknya 4 bentuk sejinis. Perhatikan lampiran. Namun hal ini tidak berlaku pada segi n beraturan yg lain. Perhatikan gambar lampiran.