
SOAL PELATIHAN DAN PEMBAHASAN MODUL PEMBELAJARAN JARAK JAUH MATEMATIKA KELAS 9 TAHUN 2021 KESEBANGUNAN
Pelatihan
- Perhatikan Sketsa Taman Sudut berbentuk trapesium siku-siku.
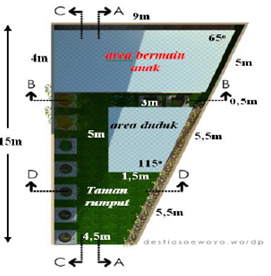
Berdasarkan sketsa tersebut, jawablah pertanyaan-pertanyaan berikut.
a. Apakah area duduk dan area bermain sebangun? Berilah penjelasan.
b. Apakah area duduk dan keseluruhan taman sebangun? Berilah penjelasan.
Jawaban:
a. Pada sketsa taman, area duduk dan area bermain masing-masing berbentuk
trapesium siku-siku. Kedua trapesium tersebut, sudut-sudut yang bersesuaian
sama besar, tetapi perbandingan sisi-sisi yang bersesuaian tidak sama
(5/4 ≠ 3/9 ≠ 5,5 / 5). Kesimpulannya adalah area duduk dan area bermain
tidak sebangun.
Perhatikan gambarnya!
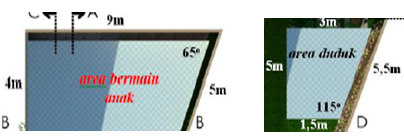
b. Pada sketsa taman, area duduk dan keseluruhan taman masing-masing
berbentuk trapesium siku-siku. Kedua trapesium tersebut, sudut-sudut yang
bersesuaian sama besar, dan memiliki perbandingan sisi-sisi yang bersesuaian
yang sama, yaitu 5/15 = 3/9 = 5,5 / 16,5 = 1,5 / 4,5 Kesimpulannya adalah
bahwa area duduk dan keseluruhan taman sebangun.
2. Perhatikan blok logika berikut ini.
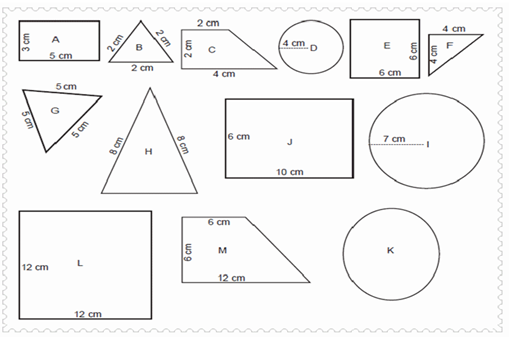
Di antara bangun-bangun tersebut, tentukan pasangan bangun yang sebangun.
Berilah alasan, mengapa pasangan bangun yang Ananda pasangkan tersebut
sebangun?
Jawaban:
Pada soal ini ada 13 bangun datar dengan berbagai bentuk, dan dari bangunbangun
tersebut harus ditentukan pasangan bangun yang sebangun.
Dengan mencermati sisi-sisi bersesuaian memiliki perbandingan yang sama dan
sudut-sudut yang bersesuaian besarnya sama, pasangan bangun yang sebangun
adalah
• bangun A dengan J;
• bangun B dengan G (dua segitiga sama sisi pasti sebangun);
• bangun C dengan M;
• bangun D dengan I (dua lingkaran pasti sebangun); dan
• bangun E dengan L (dua persegi pasti sebangun)
- Lukisan legendaris terpasang pada bingkai pigura yang berukuran 120cm x
80cm seperti tampak berikut ini. Bingkai pigura dan lukisan yang terpasang
sebangun.
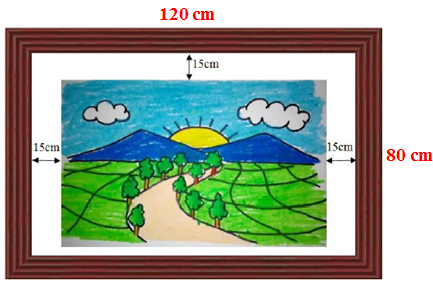
Rifat pemilik lukisan ini menginginkan posisi lukisan pada tepi atas dan tepi
bawahnya berjarak sama terhadap bingkai, tetapi Rifat belum mengetahui ukuran
lukisan dan jarak tepi bawah terhadap bingkai tersebut.
Pertanyaan 1
Berapa ukuran lukisan tersebut? Lengkapi jawaban Ananda dengan pembahasan.
Pertanyaan 2
Berapa jarak tepi bawah lukisan terhadap bingkai? Lengkapi jawaban Ananda
dengan pembahasan.
Pertanyaan 3
Untuk memenuhi keinginan Rifat, berapa centimeter masing-masing jarak tepi
atas dan tepi bawah lukisan terhadap bingkai? Lengkapi jawaban Ananda dengan pembahasan
Pembahasan:
Pada lukisan legendaris tersebut diketahui ukuran bingkai pigura 120cm x 80cm,
dan jarak tepi kiri, kanan, dan atas lukisan terhadap bingkai 15cm. Rifat
menginginkan jarak tepi atas dan tepi bawah lukisan terhadap bingkai sama.
Pertanyaan 1
Ukuran lukisan dapat ditentukan dengan cara berikut.
Panjang lukisan = 120 – (15 + 15) cm = (120 – 30)cm = 90cm
karena bingkai dan lukisan sebangun, maka dapat Ananda hitung lebar lukisan
dengan membandingkan sisi-sisi yang bersesuaian, yaitu:

Pertanyaan 2
Jarak tepi bawah lukisan terhadap bingkai adalah
= 80 – (15 + 60)cm = (80 – 75)cm
= 5cm.
Pertanyaan 3
Jarak tepi atas dan tepi bawah lukisan terhadap bingkai dapat dihitung dengan
cara :
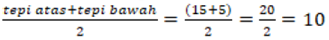
Jadi agar tepi atas dan tepi bawah lukisan berjarak sama terhadap bingkai,
masing-masing tepi atas dan bawah berjarak 10cm.
Selamat belajar semoga bermanfaat.







