
Uji Kompetensi 4 Kekongruenan dan Kesebangunan Semester 2
1. Perhatikan gambar di bawah ini. Tulislah pasangan bangun yang kongruen.
2. Jika PQRS kongruen dengan TUVR dan RT 3/5 RQ . tentukan panjang PQ.
3. Persegi panjang ABCD dibentuk dari 5 persegi panjang yang kongruen. Jika keliling setiap persegi panjang kecil adalah 20 cm, maka tentukan keliling dan luas ABCD
4. Diketahui trapesium ABCD dan trapesium FEHG pada gambar di bawah ini adalah kongruen. Jika panjang AD = 12 cm, DC = 9 cm, dan EF = 18 cm, tentukan panjang CB.
5. Pasangan bangun di bawah ini kongruen. tentukan nilai x dan y pada gambar
6. Berapa banyak pasangan segitiga kongruen pada setiap bangun di atas? Tuliskan semua pasangan segitiga kongruen tersebut.
7. Apakah pasangan segitiga berikut ini pasti kongruen? Jika ya, kriteria apakah yang menjamin pasangan segitiga berikut ini kongruen?
8. Tuliskan satu pasangan segitiga kongruen pada setiap bangun berikut dan tunjukkan
9. Perhatikan gambar. diketahui segitiga PQR kongruen dengan segitiga LKM dan m sudut PQR = 60 derajat tentukanlah
a. besar m sudut prq
b. besar m sudut LKM
c. besar m sudut KML
d. panjang KL
e. panjang KM
10. Perhatikan gambar di samping. Diketahui AC=AE dan m sudut BAC=m sudut DAE.a.buktikan bahwa ∆ABC kongruen dengan ∆ADE
b.jika CD=2 cm dan AE=10cm
c.tentukanlah panjang BC dan AB
11. Diketahui panjang AB = 13 cm dan EF = 5 cm.
a. Buktikan bahwa segititga AFE ≅ ∆DFE
b. Buktikan bahwa segitiga ≅ ∆DFE
c. Hitunglah panjang AC
d. Hitunglah panjang AE
12. apakah bangun dibawah ini pasti sebangun? jelaskan . A.dua persegi B.dua lingkaran C.dua segitiga sama sisi D.dua belah ketupat
13. Trapesium ABCD sebangun dengan trapesium RSPQ, tentukan nilai x dan y pada gambar di bawah
14. Perhatikan gambar berikut ini!
a. jika trapesium (i) dan (ii) sebangun , tentukan nilai p,q,r dan s.
b. tentukan perbandingan keliling trapesium (i) dan (ii)
c. tentukan perbandingan luas trapesium (i) dan (ii)
15. Hitunglah panjang sisi yang ditanyakan pada gambar berikut ini.
a. EF = …
b. AB =
c. AE = …
d. CF =…
16. Diketahui trapesium sama kaki PQRS pada gambar di bawah ini, dengan panjang SR = 4 cm, PQ = 12 cm, dan QS = 20 cm. Tentukan panjang SO.
17. a. Tuliskan pasangan segitiga sebangun pada gambar tersebut.
b. Dari tiap-tiap pasangan segitiga sebangun tersebut, tentukan pasangan sisi yang bersesuaian dan buat perbandingannya.
c. Tentukan panjang NK, KL, dan MK.
18. Abcd adalah persegi.
jika DE=CF,maka tentukanlah panjang:
a.DE
b.OE
c.OD
d.OC
e.OF
19. Hitunglah panjang sisi yang diberi label pada gambar di bawah ini
20. Dua belas tusuk gigi disusun seperti pada gambar di samping. Dengan memindahkan hanya dua tusuk gigi bagaimana kamu membentuk enam persegi atau tujuh persegi?
21. Enam belas tusuk gigi disusun seperti gambar di samping. Dengan memindahkan hanya dua tusuk gigi bagaimana kamu membentuk empat persegi?
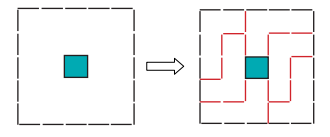
22. Pada gambar di samping ini menunjukkan persegi yang dibentuk dengan 20 tusuk gigi. Di tengahnya terdapat lubang kotak dengan luas 1/25 luas seluruhnya. Dengan menggunakan 18 tusuk gigi, bagilah luasan di antara persegi luar dan persegi di tengah menjadi 6 daerah yang sebangun.
23. bangun PINK,NOTE,dan BLUE adalah persegi. panjang KN=5cm,NE=9cm titik p – o – b terletak dalam suatu garis lurus tentukan panjang sisi dan luas bangun BLUE
24. Pada gambar di bawah ini, tinggi tongkat PQ sesungguhnya adalah 4 m dan panjang bayangannya 15 m. Jika panjang bayangan pohon adalah 30 m, tentukan tinggi pohon.
25. Sekelompok peserta jelajah alam mendapat tugas untuk menaksir lebar suatu sungai tanpa mengukurnya secara langsung. Mereka menentukan titik acuan di seberang sungai yaitu titik A. Satu peserta lain berdiri di titik C. Peserta yang lain berdiri di titik B tepat di depan A. Kemudian berjalan menuju ke titik F dengan jarak B ke F adalah dua kali jarak B ke C. Dari titik F ia berjalan menuju titik D, di mana dengan pandangannya objek di titik A-C-D terletak pada satu garis lurus. Sehingga lebar sungai dapat diketahui dengan mengukur jarak F ke D. Apakah cara tersebut tepat utuk menaksir lebar sungai? Jelaskan.
Kunci Jawaban Uji Kompetensi 4 Kekongruenan dan Kesebangunan Halaman 261 Semester 2
1. B kongruen F
G kongruen J
A kongruen K
C kongruen M
H kongruen E
2. Diketahui :
kongruen artinya sisinya sama
RT 3/5 RQ
Ditanya :
panjang PQ = ?
Jawab
RT = PQ
PQ = 3/5 x 8
= 24/5
= 4,8 cm
Jadi panjang PQ adalah 4,8 cm
3. Maka, perbandingan antara p : l adalah 4 : 1.
“p” dari persegi panjang kecil :
= 20/2 × 4/(4 + 1)
= 10 × 4/5
= 8 cm
“l” dari persegi panjang kecil :
= 20/2 × 1/(4 + 1)
= 10 × 1/5
= 2 cm
Untuk menentukan keliling ABCD, bisa kita lihat sisi lebar (tegak) – nya adalah 5 kali lipat dari lebar persegi panjang kecil. Maka, lebar ABCD :
= 5 × 2
= 10 cm
Sisi panjang persegi panjang besar sama dengan sisi panjang persegi panjang kecil. Maka, panjangnya adalah 8 cm.
Keliling :
= 2(p + l)
= 2(8 + 10)
= 2(18)
= 36 cm
Luas :
= p × l
= 8 × 10
= 80 cm²
4. panjang AB = EF = 18 cm
untuk mencari panjang CB kita gunakan pythagoras
CB² = AD² + (AB – CD)²
CB² = 12² + (18 – 9)²
CB² = 12² + 9²
CB² = 144 + 81
CB² = 225
CB = √225
CB = 15 cm
jadi panjang CB adalah 15 cm
5. Kesebangunan
Lihat kesesuaian tempat
(ii)
x = 85°
y = 360° – (85° + 70° + 125°)
y = 80°
(i)
x = 180° – 110° = 70°
y = 180° – 128° = 52°
6.

7. a. Iya, dijamin kongruen dengan kriteria sisi – sudut – sisi
b. Iya, dijamin kongruen dengan kriteria sudut 90o – sisi miring – satu sisi siku (kekongruenan khusus segitiga siku-siku)
c. Iya, dijamin kongruen dengan kriteria sudut – sisi – sudut
d. Iya, dijamin kongruen dengan kriteria sudut – sisi – sudut atau kriteria sisi – sudut – sudut
e. Iya, dijamin kongruen dengan kriteria sisi – sudut – sisi
Ya segitiga no.7 berbentuk kongruen karena kedua sisinya berukuran sama dan berbentuk sisi,sudut,sisi
8. Dua segitiga kongruen jika memenuhi kaidah:
- Sisi-sisi-sisi
Kedua segitiga memiliki tiga pasang sisi bersesuaian, yang setiap pasangannya memiliki panjang yang sama. - Sudut-sisi-sudut
kedua segitiga memiliki pasangan sudut – sisi – sudut bersesuaian dan berurutan yang besarnya sama. - Sisi-sudut-sisi
Kedua segitiga memiliki pasangan sisi – sudut – sisi bersesuaian dan berurutan yang besarnya sama.
a. Segitiga PQN kongruen dengan segitiga PRM.
Bukti:
Diketahui:
PM = PN
PQ = PR
Dari gambar bisa terlihat bahwa sudut QPN = sudut RPM karena berimpit.
Menurut kaidah sisi-sudut-sisi, kedua segitiga tersebut kongruen.
b. segitiga PSR kongruen dengan segitiga PQX.
Bukti:
Perhatikan bahwa:
PX = SR
segitigag PQR sama sisi sehingga PR = PQ
SR//PQ, maka sudut SRP = sudut RPQ karena merupakan pasangan sudut dalam berseberangan.
Menurut kaidah sisi-sudut-sisi kedua segitiga di atas kongruen.
c. Contoh: ∆ABC ≅ ∆CDA
AB//DC, AD//BC akibatnya AB = CD dan AD = CB
AC (pada ∆ABC) = AC (pada ∆CDA)
Jadi, ∆ABC ≅ ∆CDA (berdasarkan kriteria sisi – sisi – sisi)
Pembuktian ∆ABC ≅ ∆CDA juga bisa dengan kriteria sudut – sisi – sudut
m∠BAC = m∠DCA (berseberangan dalam, karena AB//DC)
AC (pada ∆ABC) = AC (pada ∆CDA) (berhimpit)
m∠ACB = m∠CAD (berseberangan dalam, karena AB//DC)
Jadi, ∆ABC ≅ ∆CDA (berdasarkan kriteria sudut – sisi – sudut)
(pasangan segitiga kongruen yang lain silakan dicari dan dibuktikan)
9. Diketahui
1)jumlah semua sudut segitiga =180
2)PQR=LKM=m=60
3)Jika diamati sudut RPQ merupakan siku2 = 90
A.
<PRQ
Maka
<PRQ
=180-60-90
=30 derajat
B
<LKM
Diatas sudah diterangkan bahwa ;
<LKM=<PQR=m=60
Maka besar sudutnya 60 derajat
C
<KML
180-60-90
=30 derajat
D.
Panjang KL
Segitiga PQR dan LKM merupakan segitiga yang kongruen maka sisinya sama =13 cm
E.
KM
=12
10. a) Membuktikan bahwa ∆ ABC kongruen dengan ∆ ADE
AE = AC (diketahui)
∠ BAC = ∠ DAE (diketahui, ada tanda pada sudut)
∠ ABC = ∠ ADE (diketahui, sudut siku-siku)
Jadi kreteria ∆ ABC kongruen dengan ∆ ADE adalah sisi – sudut – sudut
b). jika CD = 2 cm dan AE = 10cm
c). Menentukan panjang BC dan AB
AB = AC – CD
AB = 10 – 2 = 8 cm
Jadi panjang AB adalah 8 cm
BC² = AC² – AB²
BC² = 10² – 8²
BC² = 100 – 64
BC² = 36
BC = √36
BC = 6 cm
Jadi panjang BC adalah 6 cm
11. A. Segitiga AFE kongruen Segitiga DFE
bukti :
AF = AD (ada tanda sama panjang)
EF = EF (garis yang sama)
Sudut AFE = 90
Sudut EFD = 180 – 90 = 90
Sudut AFE = EFD
Kesimpulan kongruen bedasarkan teorema sisi – sudut – sisi
B. Segitiga DCB kongruen Segitiga DFE
FD = CD (ada tanda sama panjang)
BD = DE ( ada tanda sama panjang)
Segitiga DCB segitiga siku-siku
Segitiga DFE segitiga siku-siku
Kesimpulan kongruen berdasarkan teorema segitiga siku2
12. yg pasti sebangun adalah
A,B,C
karena berapapun panjang sisinya pasti perbandingan luas & kelilingnya sama
D, belah ketupat belum tentu sebangun
karena panjang sisinya ditentukan oleh panjang diagonal²nya.
13. 15 per 10 = 21 per x
kali silang menjadi
15 kali x = 21 x 10
15x = 210
x = 210 dibagi 15
x= 14
14. A. Diketahui dua trapesium dalam soal adalah sebangun. Maka untuk mengetahui nilai p, q, r, dan s diperlukan perbandingan kesebangunan.
• 12/p = 8/12 >> 8p = 144, maka p = 18 cm
• q/27 = 8/12 >> 12q = 216, maka q = 18 cm
• Untuk r, karena r merupakan sisi miring, kita akan menggunakan theorema phythagoras dari panjang sisi tegak 8 cm dan sisa panjang sisi q (perhatikan gambar terlampir).
r = √(8² + 6²)
= √(64 + 36)
= √100
r = 10 cm
• r/s = 8/12
10/s = 8/12 >> 8s = 120, maka s = 15 cm
Jadi, panjang p, q, r dan s masing – masing adalah 18 cm, 18 cm, 10 cm dan 15 cm.
B. Keliling trapesium (i) = a + b + c + d
= 12 + 10 + 18 + 8
= 48 cm
Keliling trapesium (ii) = a + b + c + d
= 18 + 15 + 27 + 12
= 72 cm
Perbandingan keliling trapesium (i) dan (ii) adalah 48 cm : 72 cm = 2 : 3 setelah semua ruas dibagi 24.
C. Luas trapesium (i) = ½ (a + b) t
= ½ (12 + 18) 8
= 120 cm²
Luas trapesium (ii) = ½ (a + b) t
= ½ (18 + 27) 12
= 270 cm²
Perbandingan luas trapesium (i) dan (ii) adalah 120 cm² : 270 cm² = 4 : 9 setelah kedua ruas dibagi 30.
15. a. 6/10 = x/8
= 10x = 48
x = 4,8
b. 4/7 = x/6
= 7x = 24
x = 34,2
c. x/9 = 2/6
= 6x = 18
EC = 3
jadi, AE = 9-3 = 6
d. x/x+4 = 5/7
5x+20 = 7x
-2x = -20
x = 10
e. f nya yg mana?
f. 6/9 = x/6
9x = 36
x = 4
maka, EF = 4+2 = 6
16. Diketahui:
panjang SR = 4 cm,
PQ = 12 cm,
QS = 20 cm.
Ditanyakan:
Panjang SO = ?
Jawab:
Perhatikan bahwa segitiga PQO dan segitiga SRO sebangun.
Kita gunakan perbandingan sisi-sisi bersesuaian untuk memperoleh panjang SO.
PQ : SR = QO : SO
↔ PQ : SR = (QS – SO) : SO
↔ 12 : 4 = (20 – SO) : SO
↔ 12SO = 4(20 – SO)
↔ 12SO = 80 – 4SO
↔ 12SO + 4SO = 80
↔ 16SO = 80
↔ SO = 80/16 = 5
Jadi, panjang SO = 5 cm
17. a. ∆ KLN sebangun dg ∆ KNM sebangun dg ∆ KLM
b.
LN : NK = NK : NM = KL : KM
c.
NK² = LN × NM
NK² = 9 × 16
NK² = 144
NK = √144
NK = 12 cm
KL² = LN × LM
KL² = 9 × (9 + 16)
KL² = 9 × 25
KL = √9 × √25
KL = 3 × 5
KL = 15 cm
MK² = NM × LM
MK² = 16 × 25
MK = √16 × √25
MK = 4 × 5
MK = 20 cm
18. DE² = CD² + CE²
DE² = 8² + (8-2)²
DE² = 64 + 36
DE² = 100
DE = √100
DE = 10 cm
OE = 3,6 cm, OD = 6,4 cm, OC = 4,8 cm, OF = 5,2 cm
19. Gambar 1:
PQ = 15
PT = 9
TR = 12
QR = 30
PR = PT + TR = 9 + 12 = 21
PST//PQR
a/PQ = PT/PR
a/15 = 9/21
a = 9×15/21
a = 6,43
b/PT = QR/PR
b/9 = 30/21
b = 30×9/21
b = 12,86
Gambar 3:
EF : AB = CF : CB
↔ 6 : 9 = 8 : (8 + p)
↔ 6(8 + p) = 9 × 8
↔ 48 + 6p = 72
↔ 6p = 72 – 48
↔ 6p = 24
↔ p = 24/6 = 4
FB : BC = FG : CD
↔ 4 : 12 = q : 24
↔ 12q = 4 × 24
↔ 12q = 96
↔ q = 96/12 = 8
Gambar 4:
SO : RO = TO : QO
↔ 10 : 18 = 14 : x
↔ 10x = 18 × 14
↔ 10x = 252
↔ x = 252/10 = 25,2
ST : QR = SO : RO
↔ 16 : y = 10 : 18
↔ 10y = 16 × 18
↔ 10y = 288
↔ y = 288/10 = 28,8
ST : QR = PS : PQ
↔ 16 : 28,8 = 12 : (12 + z)
↔ 16(12 + z) = 28,8 × 12
↔ 192 + 16z = 345,6
↔ 16z = 345,6 – 192
↔ 16z = 153,6
↔ z = 153,6/16 = 9,6
20. Gambar di samping bisa dikatakan terdiri atas 6 persegi yaitu 2 persegi besar dan 4 persegi kecil. Dapat juga dikatakan terdiri atas 7 persegi yaitu 3 persegi besar dan 4 persegi kecil.
21. 1). Pindahkan tusuk gigi bagian sudut atas kemudian bagian sudut bawah
2). Letakka kembali tusuk gigi tersebut di bagian tengah maka berbentuklah.
22.
23. persegi PINK ⇒ KN = 5 cm
persegi NOTE ⇒ NE = 9 cm
segitga OPI ⇒ PI = KN = 5 cm
OI = NO – NI
OI = 9 – 5 = 4 cm
segitiga BOT ⇒ OT = 9 cm
Kita akan menggunakan dua segitiga sebangun untuk mencari panjang BT agar selanjutnya bisa menentukan panjang sisi BE.
sisi-sisi yg bersesuaian mempunyai perbandingan yg sama pada Δ OPI dan Δ BOT.
PI / OT = OI / BT = PO / OB
PI / OT = OI / BT
5 / 9 = 4 / BT
5 BT = 4 × 9
5 BT = 36
BT = 36 / 5
BT = 7,2 cm
panjang BE = BT + TE
= 7,2 cm + 9 cm
= 16,2 cm
Luas persegi BLUE = 16,2 cm × 16,2 cm
= 262,44 cm²
Jadi luas bangun BLUE adalah 262,44 cm²
24. Diketahui :
Tinggi tongkat PQ = 4 m
Panjang bayangan tongkat OQ = 15 m
Panjang bayangan pohon OR = 30 m
Ditanya :
Tinggi pohon SR ?
Jawab :
Δ QOP sebangun dengan Δ ROS
Sisi-sisi yg bersesuaian
• OQ dengan OR
• PQ dengan RS
Menentukan tinggi pohon
OQ/OR = PQ/SR
15/30 = 4/SR
15 SR = 30 × 4
15 SR = 120
SR = 120/15
SR = 8
Jadi tinggi pohon tersebut adalah 8 m
25. Iya, tentu. Cara tersebut menggunakan konsep kekongruenan dua segitiga dalam gambar di samping yaitu ∆ABC dan ∆DFC. Silakan dibuktikan. Petunjuk: gunakan kriteria kekongruenan sudut-sisi-sudut (gunakan titik sudut B, C, dan F dan sisi BC dan FC)






