SOAL DAN PEMBAHASAN BUKU SISWA MATEMATIKA KELAS 8 SEMESTER 2 LATIHAN 6.1 HALAMAN 11 TAHUN 2021
- Gunakan teorema Pythagoras untuk menentukan nilai yang belum diketahui pada masing-masing gambar berikut.
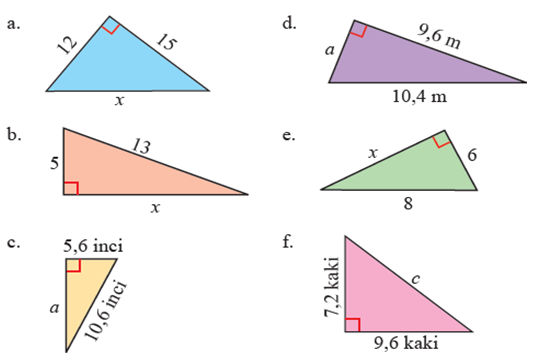
Pembahasan:
a. x2 = 122 + 152
x2 = 144 + 225
x2 = 369
x = √369
b. x2 = 132 – 52
x2 = 169 – 25
x2 = √144
x = 12
c. a2 = (10,6)2 – (5,6)2
a2 = 112,36 – 31,36
a2 = 81
a = √81 = 9 inci
d. a2 = (10,4)2 – (9,6)2
a2 = 108,16 – 92,16
a2 = 16
a = √16 = 4 m
e. x2 = 82 – 62
x2 = 64 – 36
x2 = 28
x = √28
f. c2 = (7,2)2 + (9,6)2
c2 = 51,84 + 92,16
c2 = 144
c = √144 = 12 kaki
- Tujuan dipasangkan kawat bubut pada suatu tiang telepon adalah untuk menopangnya. Kawat
bubut dipasang pada tiang telepon setinggi 8 m dari tanah ,
a. Jelaskan cara yang akan kalian lakukan untuk menentukan panjang kawat bubut tanpa
mengukur langsung kawat tersebut.
b. Tentukan panjang kawat jika jarak antara kawat dan tiang pada tanah dalam 6 meter.

Pembahasan:
a. Tiang listrik dan tanah datar membentuk sudut siku-siku, sehingga terbentuk segitiga siku-siku.
Pada segitiga siku-siku berlaku rumus Pyhtagoras untuk mencari panjang sisi yg lain tanpa
harus mengukur langsung.
b. Misalkan : a = tinggi tiang yg dipasang kawat dari tanah
b = jarak pada tanah
c = panjang kawat bubut
c² = a² + b²
c² = 8² + 6²
c2 = 64 + 36= 100
c = √100 = 10 m
Sehingga panjang kawat bubut adalah 10 m
3. Tentukan nilai x pada kedua gambar berikut.
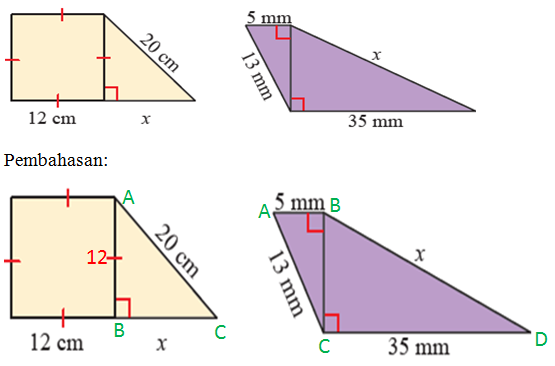
a. Perhatikan segitiga ABC gambar kiri
BC2 = AC2 – AB2
x2 = 202 – 122
x2 = 400– 144
x2 = 256
x = √256 = 16 cm
b. Perhatikan segitiga ABC gambar kanan
BC2 = AC2 – AB2
BC2 = 132 – 52
BC2 = 169– 25
BC2 = 144
BC = √144 = 12 cm
Perhatikan segitiga BCD gambar kiri
BD2 = BC2 + CD2
x2 = 122 + 352
x2 = 144+ 1225
x2 = 1369
x = √1369 = 37 cm
4. Apakah suatu segitiga yg panjang ketiga sisinya berturut-turut 9cm,12cm,dan 18cm merupakan
segitiga siku-siku ? Jelaskan!
Pembahasan:
Diketahui a = 9 cm, b = 12 cm, dan c = 18 cm.
a² + b² = c²
⇔ 9² + 12² = c²
⇔ 81 + 144 = c²
⇔ c² = 225
⇔ c = 15 cm
Jadi, suatu segitiga yang panjang ketiga sisinya berturut-turut 9 cm, 12 cm, dan 18 cm bukan
segitiga siku-siku, karena nilai c = 15 cm. Supaya membentuk segitiga siku-siku maka
nilai c harus 18 cm.
5. Jika panjang sisi suatu segitiga siku siku berturut turut adalah x, 15 dan x+15, tentukan nilai x.
Pembahasan:
a² + b² = c² Rumus Pythagoras
x² + 15² = (x + 5)²
x² + 225 = x² + 10x + 25
x² – x² – 10x = 25 – 225
-10x = -200
x = -200 : -10
x = 20
6. Tentukan panjang AB dari gambar berikut.
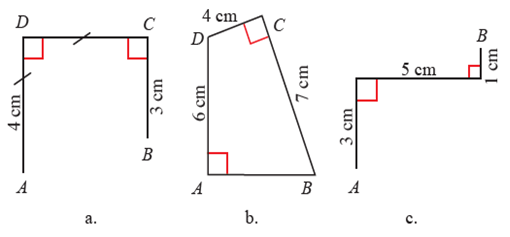
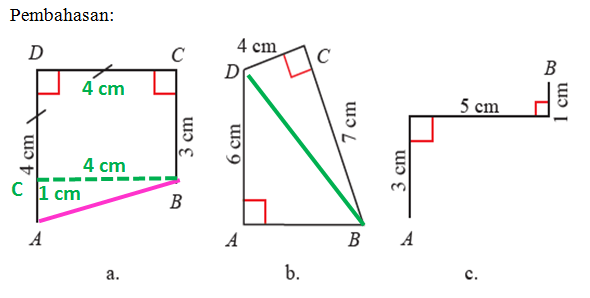
a. Perhatikan gambar a
BC = 3 cm
CD = 4 cm
DA = 4 cm
Sehingga
AB² = CD² + (AD – BC)²
AB² = 4² + (4 – 3)²
AB² = 16 + 1
AB² = 17
AB = √17
Jadi Panjang AB = √17 cm
Cara lain:
AB2 = BC² + AC²
AB2 = 4² + 1²
AB² = 16 + 1
AB² = 17
AB = √17
Jadi Panjang AB = √17 cm
b. Perhatikan gambar b
BC = 7 cm,
CD = 4 cm
AD = 6 cm. Sehingga
BD² = BC² + CD²
BD² = 7² + 4²
BD² = 49 + 16
BD² = 65
BD = √65
Langkah selanjutnya
BD² = AB² + AD²
AB² = BD² – AD²
AB² = (√65)² – 6²
AB² = 65 – 36
AB² = 29
AB = √29
Jadi, panjang AB adalah √29 cm.
c. Perhatikan gambar c
AC = 3 cm,
CD = 5 cm
BD = 1 cm
Semua titik kita hubungkan dan membentuk segi empat, sehingga
AF = BE = 3 + 1 = 4 cm.
CD = AE = BF = 5 cm.
Langkah selanjutnya
AB² = AE² + BE²
AB² = 5² + 4²
AB² = 25 + 16
AB² = 41
AB = √41
Jadi, panjang AB adalah √41 cm.
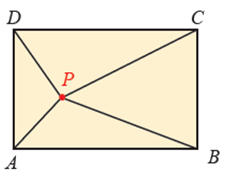
7. Diketahui persegi panjang ABCD dan P merupakan titik di dalam persegi panjang.
Jika PC = 8 cm, PD = 4 cm & PB = 7 cm, maka PA adalah?
Pembahasan :
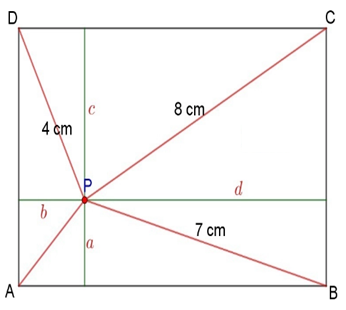
Diketahui :
PC = 8 cm
PD = 4 cm
PB = 7 cm
Ditanyakan : panjang PA = ?
Perhatikan gambar persegi panjang yang ada pada lampiran
Pada gambar persegi panjang ABCD, kita lihat
∠ APB, ∠ BPC, ∠ CPD dan ∠ APD tidak ada yang siku-siku.
Jadi Δ CPD dan Δ APB tidak bisa kita pythagoraskan langsung.
Kita tarik garis hitam yang tegak lurus melalui titik P agar terbentuk segitiga siku-siku, karena
syarat pythagoras adalah salah satu sudut pada segitiga haruslah siku-siku dan kedua sisi tegak lurus.
Ada 4 garis diagonal yang terdiri dari 4 segitiga siku-siku
Keempat diagonal tersebut kita masukan kedalam rumus pythagoras yaitu c² = a² + b², maka PA² = a² + b²
PD² = b² + c²
4² = b² + c²
b² = 4² – c²
PC² = c² + d²
8² = c² + d²
c² = 8² – d²
PB² = a² + d²
7² = a² + d²
a² = 7² – d²
PA² = a² + b²
PA² = (7² – d²) + (4² – c²)
PA² = 7² – d² + 4² – (8² – d²)
PA² = 7² – d² + 4² – 8² + d²
PA² = 7² + 4² – 8²
PA² = 49 + 16 – 64
PA² = 65 – 64
PA² = 1
PA = √1
PA = 1 cm
Jadi panjang PA adalah 1 cm
Cara lain :
PA² + PC² = PD² + PB²
PA² + 8² = 4² + 7²
PA² = 4² + 7² – 8²
PA² = 16 + 49 – 64
PA² = 65 – 64
PA² = 1
PA = 1 cm
Jadi panjang PA adalah 1 cm
8. Seorang yang bernama Bhaskara menyusun sebuah persegi dan empat buah segitiga siku siku
yang memiliki panjang sisi yang sama yaitu a,b,dan c kedalam sebuah persegi yang mempunyai
panjang sisi c.
a. Tunjukan bagaimana kelima potong bangun datar yang disusun pada gambar bagian tengah
dapat disusun untuk mengisi bangun yang paling kanan.
b. Jelaskan bagaimana teorema pythagoras termuat dalam pertanyaan a
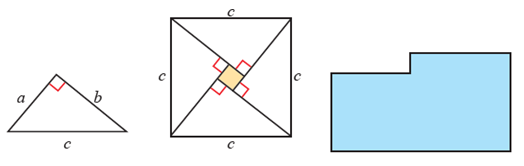
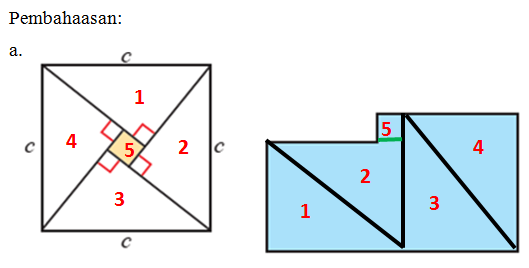
b. Teorema Pythagoras dipertanyakan
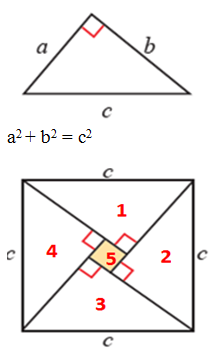
Pada gambar didapatkan
4 luas segitiga + luas yang diarsir no 5 = luas persegi besar
4 . ½ .ab + (b – a)2 = c2
2ab + b2 – 2ab + a2 = c2
a2 + b2 = c2
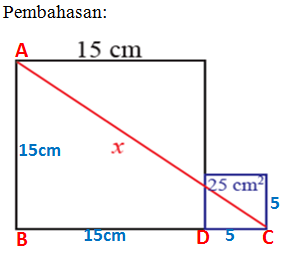
9. Perhatikan gambar dua persegi di samping. Panjang sisi persegi besar adalah 15 cm.
Luas persegi kecil adalah 25 cm². Tentukan nilai x
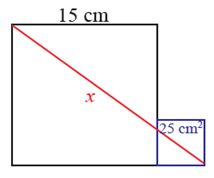
Gunakan rumus teorema pythagoras : a² + b² = c²
dengan a dan b sisi pada siku-sikunya dan c adalah sisi terpanjang (sisi miring)
dalam gambar, persegi besar dengan sisi 15 cm, dan persegi kecil dengan luas 25 cm²
kita cari panjang sisi persegi kecil = √25 = 5 cm
Perhatikan gambar segitiga dalam gambar soal,
alas segitiga = panjang sisi persegi besar + panjang sisi persegi kecil
= 15 + 5
= 20 cm
tinggi segitiga = panjang sisi persegi besar
= 15 cm
nilai x = …?
gunakan teorima pythagoras
(alas segitiga)² + (tinggi segitiga)² = x²
20² + 15² = x²
x² = 400 + 225
x² = 625
x = √625
x = 25 cm
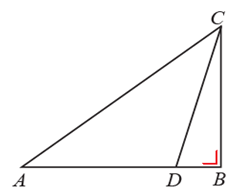
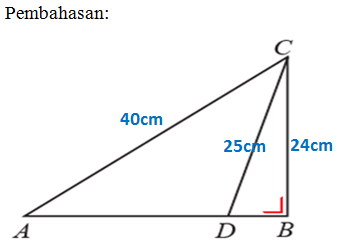
10. Perhatikan gambar di samping. Diketahui ABC siku siku di B dengan panjang AC=40 cm dan
BC=24 cm.Titik D terletak pada AB sedemikian sehingga CD=25 cm.Panjang AD adalah….cm.
Diketahui:
Segitiga ABC siku-siku di B
Panjang AC = 40 cm dan BC = 24 cm
Titik D terletak pada AB sedemikian sehingga CD = 25 cm.
Ditanyakan: Panjang AD adalah ….
Jawab:
Perhatikan gambar!
Garis CD akan membentuk segitiga BCD siku-siku di B.
Untuk segitiga ABC siku-siku di B:
AB² = AC² – BC²
AB2 = 40² – 24²
AB2 = 1.600 – 576
AB2 = 1.024
AB = √1.024 = 32 cm
Untuk segitiga BCD siku-siku di B:
BD² = CD² – BC²
= 25² – 24²
= 625 – 576
= 49
BD = √49 = 7 cm
Titik D pada AB, maka:
AD = AB – BD
= 32 – 7
= 25 cm Jadi, panjang AD adalah 25 cm