Ayo Kita Berlatih 6.4 Semester 2
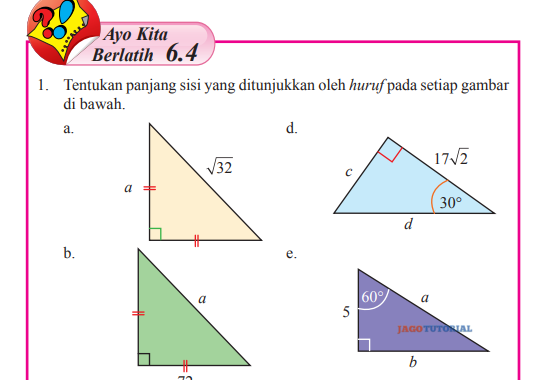
1. Tentukan panjang sisi ditunjukkan oleh huruf pada setiap gambar dibawah
2. Tentukan keliling persegi abcd berikut
3. Tentukan luas segitiga berikut.
4. Apa yang salah dengan gambar di bawah ini? Jelaskan
5. Tentukan luas persegi panjang KLMN berikut!
6. Perhatikan gambar segitiga siku-siku ABC di bawah. Tentukan: a. keliling segitiga ABC, b. tentukan luas segitiga ABC.
7. Tentukan luas trapesium di bawah ini.
8. perhatikan gambar segitiga ABC di bawah ini. diketahui <ABC=90° <CDB=45°,<CAB=30°,dan AD=2cm.tentukan panjang BC.
9. Perhatikan balok ABCD.EFGH di samping jika besar sudut BCA = 60˚ ,
tentukan :
a. panjang
b. luas bidang ACGE
10. Gambar di samping adalah jaringjaring piramida segitiga.
a. Berapakah panjang b?
b. Berapakah luas permukaan piramida?
Kunci Jawaban Ayo Kita Berlatih 6.4 Halaman 40 Semester 2
1. A. a/√32=1/√2
√2×a=√32
a=√32/√2
a=√16
a=4 satuan
B. 72/a=1/√2
a=72×√2
a=72√2 satuan
C. b/16=√3/2
2b=16√3
b=(16√3)/2
b=8√3cm
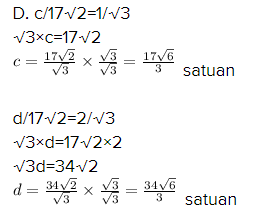
E. a/5=2/1
a=5×2
a=10 satuan
b/5=√3/1
b=5×√3
b=5√3 satuan
F. d/20=1/2
2d=20
d=20/2
d=10 satuan
e/20=√3/2
2×e=20×√3
e=(20√3)/2
e=10√3 satuan
2. Diketahui
AC = 18√2
Ditanyakan
Keliling persegi
Jawab
Misal sisi persegi panjang tersebut adalah s, maka AB = BC = CD = AD = s
Perhatikan segitiga ABC siku-siku di B, maka berdasarkan rumus pythagoras
AB² + BC² = AC²
s² + s² = (18√2)²
2s² = 18² . √4
s² = 18^2 x 2/2
s² = 18²
s = 18
Jadi keliling persegi ABCD adalah
= 4s
= 4(18)
= 72 satuan keliling
3. dalam gambar, sudut-sudut dalam segitiga itu adalah 45°, 45° dan 90°
perbandingan sisi-sisi segitiga dengan sudut istimewa 45°
∠ 45 : ∠ 45 : ∠90 = 1 : 1 : √2
diketahui panjang sisi miring atau panjang sisi yang menghadap sudut 90 adalah 16, untuk mencari luas segitiga kita cari panjang sisi-sisi siku-sikunya
panjang sisi siku-siku : panjang sisi miring = 1 : √2
panjang sisi siku-siku : 16 = 1 : √2
panjang sisi siku-siku = 1/√2 x 16
= 1/2 x √2 x 16
= 8√2
4. luas segitiga = 1/2 x panjang sisi siku-siku x panjang sisi siku-siku
= 1/2 x 8√2 x 8√2
= 4√2 x 8√2
= 32√4
= 32 x 2
= 64 satuan luas
5.

6. Segitiga siku-siku yang dimaksud bukanlah segitiga siku-siku dengan sudut 30°, 60°, dan 90°, karena perbandingan panjang ketiga sisinya tidak sama dengan 1 : 2 : 3 . √3
Perhatikan Δ ADC siku-siku di D, ∠ CAD = 60° dan ∠ ACD = 30°
AC : AD = 2 : 1
AC : 8 = 2 : 1
AC = 8 × 2
AC = 16 cm
AD : CD = 1 : √3
8 : CD = 1 : √3
8 / CD = 1 / √3
CD = 8 × √3
CD = 8√3 cm
Perhatikan Δ BDC siku-siku di D, ∠ CBD = 30° dan ∠ DCB = 60°
CD : BD = 1 : √3
8√3 : BD = 1 : √3
8√3 / BD = 1 / √3
BD = 8√3 × √3
BD = 8 × 3
BD = 24 cm
CD : BC = 1 : 2
8√3 : BC = 1 : 2
8√3 / BC = 1 / 2
BC = 8√3 × 2
BC = 16√3 cm
a. Keliling Δ ABC = AD + BD + BC + AC
= 8 cm + 24 cm + 16√3 + 16 cm
= 48 cm + 16√3 cm
= 16 (3 + √3) cm
Jadi keliling segitiga ABC adalah 16 (3 + √3) cm
b. Luas Δ ABC = 1/2 × AB × CD
= 1/2 × (8 + 24) cm × 8√3 cm
= 1/2 × 32 × 8√3 cm²
= 16 × 8√3 cm²
= 128√3 cm²
Jadi luas segitiga ABC adalah 128√3 cm²
7.

fc = 1/2√3

8. Diketahui :
Δ ABC
∠ ABC = 90 °
∠ CDB = 45°
∠ CAB = 30°
AD = 2 cm.
ditanya :
panjang BC ?

9. Diketahui :
∠ BCA = 60°
BC = CG = 24 cm
Ditanya :
a. Panjang AC ?
b. Luas bidang ACGE
Jawab :
a.
AC : BC = 2 : 1
AC : 24 = 2 : 1
AC / 24 = 2 / 1
AC = 24 × 2
AC = 48 cm
Jadi panjang AC adalah 48 cm
b.
Luas ACGE = AC × CG
= 48 cm × 24 cm
= 1152 cm²
Jadi luas bidang ACGE adalah 1152 cm²
10. Sisi b adalah sisi miring atau hipotenusa pada sebuah segitiga siku-siku sama kaki, maka untuk mencari b kita bisa menggunakan teorema phytagoras:
b²=4²+4²
b²=16+16
b²=32
b=√32
b=√(16×2)
b=4√2 cm
Sekarang perhatikan segitiga bagian alas piramida (lihat lampiran), diketahui alas segitiga nya adalah b=4√2cm. Tinggi segitiga dapat dicari dengan menggunakan teorema phytagoras:
t²=(4√2)²-(2√2)²
t²=32-8
t²=24
t=√24
t=√(4×6)
t=2√6 cm
Luas permukaan piramida=Luas alas + (3 x Luas sisi tegak)
=((1/2)×(4√2)×2√6)+(3×(1/2)×4×4)
=4√12+24
=(4√(4×3))+24
=(4×2√3)+24
=(8√3+24)cm²