Latihan 5.1 Tabung Semester 2
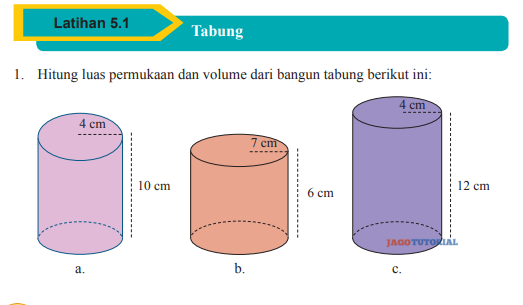
1. Hitung luas permukaan dan volume dari bangun tabung berikut ini:
2. Tentukan panjang dari unsur tabung yang ditanyakan
3. Berpikir kritis. Terdapat suatu tabung dengan jari jari r cm dan tinggi tabung t cm, dimana r < t. Misalkan tabung tersebut memiliki volume V cm dan luas permukaan L cm. Apakah mungkinv V = L? Jika ya tentukan nilai 1/r + 1/t.
4. Tantangan. Gambar disamping merupakan suatu magnet silinder. Alas dari magnet tersebut dibentuk dari dua lingkaran yang sepusat. Lingkaran yang lebih kecil memiliki jari jari r1 = 4 cm, sedangkan lingkaran yang lebih besar memiliki jari jari r2 = 6cm, Tinggi dari magnet adalah t = 10 cm. Tentukan :
a. Luas permukaan magnet
b Volume magnet
5. Misalkan terdapat suatu tabung dengan jari jari r dan panjang t. Kemudian tabung tersebut dijadikan irisan tabung dengan memotong tabung tersebut menjadi dua bagian yang sama persis dari atas ke bawah. Tentukan rumus untuk menghitung luas irisan tabung tersebut.
6. terdapat suatu tandon yang berbentuk tabung dengan jari-jari 50 cm tinggi 2 m. Tandon tersebut berisi air sebanyak 3/4 dari volume total. Terdapat lubang kecil di dasar tendon tersebut yang menyebabkan air mengalir keluar dengan kecepatan 50 cm3/detik. Air pada tandon tersebut akan habis…detik? (anggap pi=3,14).
7. Pondasi rumah. Alas dari pondasi rumah pak Ahmad berbentuk seperti gambar di samping. Jika tinggi pondasi adalah 2m maka:
a. Tentukan luas permukaan pondasi
b. Tentukan volume pondasi
8. Analisis kesalahan.Rudi menghitung volume tabung dengan diameter 5 cm dan tinggi 12 cm.Rudi menghitung
V=(12)pangkat 2 (5)=720
sehingga diperoleh volume tabung adalah 720 cm kubik.tentukan kesalagjan yang dilakukan Budi.
9. Pada gambar di bawah terdapat dua buah bangun sisi lengkung.sebelah kiri merupakan tabung dengan jari-jari r dan tinggi t. sebelah kanan merupakan bangun ruang sisi lengkung yang diperoleh dari tabung sebelah kiri dengan menggeser tutup ke sebelah kanan, selanjutnya disebut dengan tabung miring.tabung miring tersebut memiliki jari-jari r dan tinggi t.
a.) tentukan suatu metode untuk mendapatkan rumus dari volume tabung miring tersebut.
b.) apakah volume rumus tabung miring sama dengan volume tabung? jelaskan analisismu.
10. Kaleng susu. Suatu perusahaan susu memiliki kotak susu ukuran 40 cm × 60 cm × 20 cm. Kapasitas maksimal kotak tersebut adalah 48 kaleng susu. Jari-jari
kaleng susu adalah r cm dan tingginya t cm. Perusahaan tersebut membuat peraturan :
i. Nilai r dan t harus bilangan bulat
ii. Luas permukaan kaleng tersebut harus seminimal mungkin. Tentukan nilai r dan t.
Kunci Jawaban Latihan 5.1 Tabung Halaman 280 Semester 2
1. A. L = Phi × r2
= 3,14 × 4(2)
= 3,14 × 16
= 50,24 cm2
V = phi × r2 × t
= 3,14 × 4(2) × 10
= 3,14 × 16 × 10
= 502,4 cm3
B. L = phi × r2
= 22/7 × 7(2)
= 22/7 × 49
= 22 × 7
= 154 cm2
V = phi × r2 × t
= 22/7 × 7(2) × 6
= 22/7 × 49 × 6
= 22 × 7 × 6
= 924 cm3
C. L = phi × r2
= 3,14 × 4(2)
= 3,14 × 16
= 50,24 cm2
V = phi × r2 × t
= 3,14 × 4(2) × 12
= 3,14 × 16 × 12
= 602,88 cm3
d. d = 2 m dan t = 8 m
LP = 2 π r (r + t)
= 2 × 3,14 × 1 (1 + 8) m²
= 6,28 × 9 m²
= 56,25 m²
V = π r² t
= 3,14 × 1 × 1 × 8 m³
= 25,12 m³
E. lp=2πr(t+r)
(2×3,14×2)x(10+2)
12,56×12
150,72m³
itu JariJari nya 2 karna diameter nya 4m
E.volume=(3,14x2x2)X10
12,56×10
125,6m³
itu JariJari nya 2 karna diameter nya 4m
F. lp=(2×3,14×3,5)x(20+3,5)
21,98×23.5
96,93dm³
volume=(3,14×3,5×3,5)x20
38,465×20
769,3dm³
JariJari nya 3,5 soal nya diameter nya 7dm
2. Soal a.
V = 600 π ; d = 20
V = luas alas × tinggi
V = (1/4)πd² × tinggi
600 π = (1/4)π × (20²) × t
600 π = (1/4)π × 400 × t
600 π = 100 π × t
t = (600 π) / (100 π)
t = 6 …………………. tinggi = 6 cm
Soal b.
V = 120 π ; r = 5
V = luas alas × tinggi
V = π r² × tinggi
120 π = π (5²) × t
120 π = 25 π × t
t = (120 π) / (25 π)
t = 4,8 ……………………tinggi 4,8 cm
c. V = 224 π cm³ dan d = 8 cm
Volume = π r² t
224 π = π (8/2)² t
224 π = π 4² t
224 π = π 16 t
t = 224 π /16 π
t = 14 cm
Jadi tinggi tabung adalah 14 cm
d) Diketahui =
t = 13 cm
L = 528π cm²
Ditanya = r
Jawab =
L = 2πr(r+t)
528π = 2πr(r+13)
264 = r²+13r
r²+13r-264 = 0
r = 11 cm
E. Diketahui:
luas = 450 πcm²
tinggi=15cm
Ditanya :
r = ?
Jawab :
L = π × r² × t
450 π= π× r² × 15
450/15 = r ²
30 = r²
√30 = r
Jadi r = √30cm
f) Diketahui =
t = 6 cm
V = 294π m³
Ditanya = r
Jawab =
V = πr²t
294π = πr²×6
r² = 49
r = 7 cm
3. Sebuah tabung berjari-jari r cm dengan tinggi t cm.
r < t
Volume tabung = V cm³
Luas permukaan tabung = L cm²
Ditanyakan:
Apakah mungkin V = L? Jika ya tentukan nilai 1/r + 1/t.
Jawab:
V = π r² t
L = 2 π r (r + t)
Kondisi pada saat volume sama dengan luas permukaan:
V = L
↔ π r² t = 2 π r (r + t)
↔ r t = 2(r + t)
↔ (r + t)/rt = 1/2
↔ r/rt + t/rt = ½
↔ 1/t + 1/r = 1/2
Jadi, mungkin terjadi nilai V = L, yaitu ketika nilai 1/t + 1/r = ½
4. a. Luas permukaan magnet
= luas penampang luar magnet + luas penampang dalam magnet + 2(luas lingkaran b – lingkaran k)
= 2π r2 . t + 2πr1.t + 2(π r2² – π r1²)
= 2π 6 .10 + 2π 4. 10 + 2(π.6² – π.4²)
= 120π + 80π + 2(36π – 16π)
= 200π + 2(20π)
= 200π + 40π
= 240π
= 240 x 3,14 cm²
= 753,6 cm²
Jadi Luas permukaan magnet 753,6 cm²
b, Volume magnet
V = Volume tabung besar – volume tabung kecil
= π r2² .t – π r1². t
= π.6² . 10 – π 4². 10
= 3600π – 1600π
= 2000π
= 2000 x 3,14
= 6.280 cm³
Jadi Volume magnet 6.280 cm³
5. Luas permukaan tabung = 2 x luas alas + luas selimut tabung
= 2 . π . r² + 2 . π . r . t
Luas permukaan irisan adalah luas tabung : 2, ditambah dengan luas persegi panjang sbb:
Luas permukaan irisan = [(2 . π . r² + 2 . π . r . t)/2] + 2r . t
= π . r² + π . r . t + 2r . t
= r . (π.r + π.t + 2t) ⇒ Rumus Luas permukaan irisan
6. J= 50cm
T=2m=200 cm
Isi 3/4
D=50cm /s
Jawab
Vtabung = la.t
=(j.phi)t
= (50.22/7)200
=(1100/7)200
=157.200
=31400
Waktu: 31400/50
= 88 s
7. a. PERHATIKAN GAMBAR TERLAMPIR
diperoleh:
sisi persegi = 5 + 20 + 5 = 30 cm
Luas persegi = s x s
= 30 x 30
= 900 cm²
Luas permukaan tabung = 4 x 1/4 [(2 x 3,14 x 5) ( 5 + 2)]
= 31,4 x 7
= 219,8
Luas permukaan fondasi = 2x (900) – 219,8
= 1.800 – 219,8
= 1.580,2 cm²
b. Volume balok = 30 x 30 x 2
= 1800 cm³
Volume tabung = 4 x 1/4 x 3,14 x 5² x 2
= 157 cm³
Volume pondasi = 1800 – 157
= 1.643 cm³
8. Diameter(d) = 5 cm
r= 1/2 x 5 cm
r = 2,5 cm
tinggi (t) = 12 cm
rumus volume tabung = phi x r² x t
V = 3,14 x 2,5 x 2,5 x 12
V =235,5 cm ³
jadi volume tabung sebenarnya 235,5 cm³
kesalahan yang dilakukan budi yaitu salah menggunakan rumus , rumus yg digunakan budi = t² x d seharusnya rumus yg digunakan adalah = phi x r² x t
9. a. Salah satu metodenya adalah dengan membuat tumpukan koin yang
membentuk kerucut miring.
b. Sama, karena kaidah volume adalah luas alas dikalikan dengan tinggi.
Dengan mengubah kerucut menjadi kerucut miring tidak mengubah alas
dan tingginya, sehingga tidak terjadi perubahan volume.
10. volume kotak susu = p.l.t=40cm . 60cm . 20cm= 48.000cm kubik
jumlah 1 kaleng susu= 48.000cm/48 kaleng= 1000cm kubik
jadi jari-jari kaleng=tinggi kaleng=panjang rusuk kaleng
√1000=10
jadi jari-jari kaleng 10cm, tingginya 10cm
karena kaleng bervolume 1000cm diperkirakan berbentuk kubus
jadi luas permukaaan kaleng= 6 . sisi
= 6 . (10 . 10)
= 6 . (100)
= 600 cm persegi






