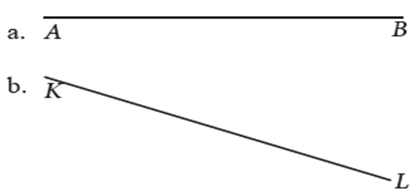
- Salinlah dua garis berikut
Kemudian dengan menggunakan jangka dan penggaris bagilah
masing-masing garis menjadi 7 bagian yang sama panjang.
Pembahasan:
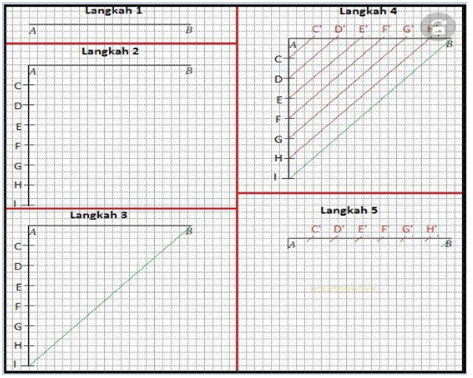
a. Gambar garis AB
Langkah-langkah kegiatan:
1) Salin garis AB dengan ukuran dan arah yang sama pada buku tulis
2) Dari titik A, buatlah garis AI dengan ukuran 7 bagian yang sama
sedemikian sehingga tidak berimpit dengan garis AB, yaitu AC =
CD = DE = EF = FG = GH = HI. Agar lebih mudah membaginya,
garis AI kita buat tegak lurus garis AB.
3) Hubungkan titik I dengan titik B
4) Buatlah garis-garis sejajar dengan ruas garis IB yang garis-garis
tersebut melalui titik C, D, E, F, G, dan H sehingga memotong garis
AB di titik C', D’, E’, F’, G’, dan H’.
5) Hapus garis-garis yang telah dibuat kecuali garis AB dan titik C', D’,
E’, F’, G’, H’.
Dengan demikian, terbagilah ruas garis AB menjadi 7 bagian yang
sama, yaitu AC’ = C'D' = D’E’ = E’F’ = F’G’ = G’H’ = H’B. Perhatikan gambarnya:
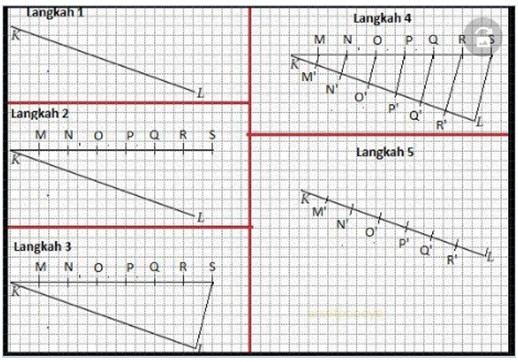
b. Gambar garis KL
Langkah-langkah kegiatan:
1) Salin garis KL dengan ukuran dan arah yang sama pada buku tulis
2) Dari titik K, buatlah garis KS dengan ukuran 7 bagian yang sama
sedemikian sehingga tidak berimpit dengan garis KL, yaitu KM =
MN = NO = OP = PQ = QR = RS. Agar lebih mudah membaginya,
garis KS kita buat mendatar (horizontal).
3) Hubungkan titik S dengan titik L
4) Buatlah garis-garis sejajar dengan ruas garis SL yang garis-garis
tersebut melalui titik M, N, O, P, Q dan R sehingga memotong garis
KL di titik M’, N’, O’, P’, Q’ dan R’.
5) Hapus garis-garis yang telah dibuat kecuali garis KL dan titik M’,
N’, O’, P’, Q’,R’.
Dengan demikian, terbagilah ruas garis KL menjadi 7 bagian yang
sama, yaitu
KM’ = M’N’ = N’O’ = O’P’ = P’Q’ = Q’R’ = R’LPerhatikan gambarnya!
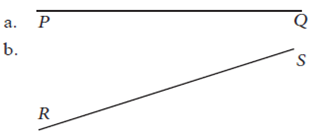
- Salinlah dua garis berikut
Kemudian bagilah masing-masing garis dengan perbandingan 2 : 3.
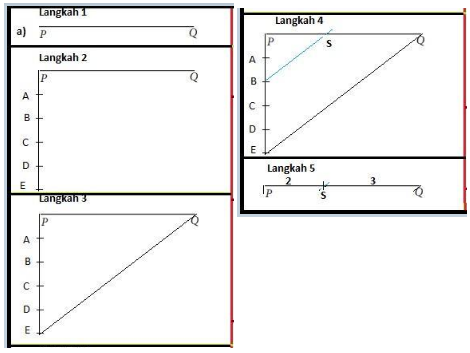
Pembahasan:
a. Gambar garis PQ
Langkah-langkah kegiatan:
1) Salin garis PQ dengan ukuran dan arah yang sama pada buku tulis
2) Dari titik P, buatlah garis PE dengan ukuran 5 bagian yang sama
sedemikian sehingga tidak berimpit dengan garis PQ, yaitu PA =
AB = BC = CD = DE sehingga PB : BE = 2 : 3. Agar lebih mudah
membaginya, garis PE kita buat tegak lurus garis PQ.
3) Hubungkan titik E dengan titik Q
4) Buatlah garis yang sejajar dengan ruas garis EQ yang melalui titik B
sehingga memotong garis PQ di titik S.
5) Hapus garis-garis yang telah dibuat kecuali garis PQ dan titik S.
Dengan demikian, terbagilah ruas garis PQ menjadi 2 bagian dengan
perbandingan PS : SQ = 2 : 3Perhatikan gambarnya:
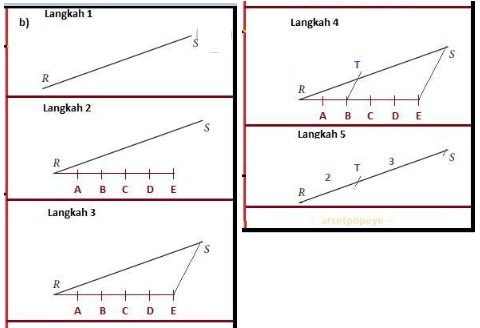
b. Gambar garis RS
Langkah-langkah kegiatan:
1) Salin garis RS dengan ukuran dan arah yang sama pada buku tulis
2) Dari titik R, buatlah garis RE dengan ukuran 5 bagian yang sama
sedemikian sehingga tidak berimpit dengan garis RS, yaitu RA =
AB = BC = CD = DE sehingga RB : BE = 2 : 3. Agar lebih mudah
membaginya, garis RE kita buat mendatar (horizontal).
3) Hubungkan titik E dengan titik S
4) Buatlah garis yang sejajar dengan ruas garis ES yang melalui titik
B sehingga memotong garis RS di titik T.
5) Hapus garis-garis yang telah dibuat kecuali garis RS dan titik T.
Dengan demikian, terbagilah ruas garis RS menjadi 2 bagian dengan
perbandingan RT : TS = 2 : 3Perhatikan gambarnya!
- Diketahui panjang ruas garis AB adalah 12 cm. Bagilah ruas garis AB
tersebut menjadi 5 bagian sama panjang.
Pembahasan:
Langkah-langkah kegiatan:
1) Buat garis AB sepanjang 12 cm, misal garisnya garis mendatar
2) Dari titik A, buatlah garis AG dengan ukuran 5 bagian yang sama
Sedemikian sehingga tidak berimpit dengan garis AB, yaitu AC =
CD = DE = EF = FG.
Agar lebih mudah membaginya, garis AG kita buat tegak (vertikal)
3) Hubungkan titik G dengan titik B
4) Buatlah garis yang sejajar dengan ruas garis GB, dimana garis-garis
tersebut melalui titik C, D, E, F sehingga memotong garis AB di titik
C’, D’, E’ dan F’.
5) Hapus garis-garis yang telah dibuat kecuali garis AB dan titik C’, D’,
E’ dan F’.
Dengan demikian, terbagilah ruas garis AB menjadi 5 bagian yang
sama yaitu AC’ = C’D’ = D’E’ = E’F’ = F’BPerhatikan gambarnya!
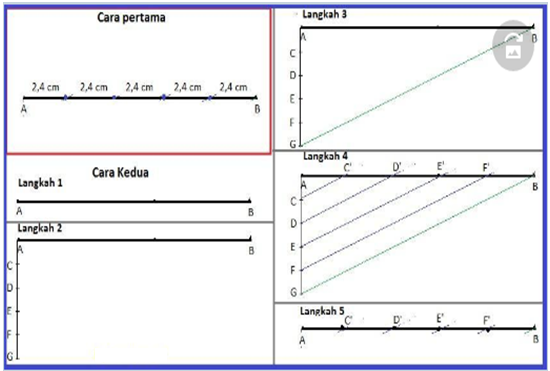
- Perhatikan gambar berikut.
Tentukan nilai p.
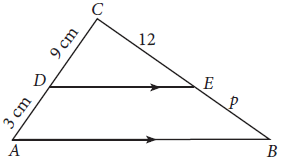
Pembahasan:
Diketahui :
AD = 3 cm
CD = 9 cm
CE = 12 cm
Ditanyakan : Nilai BE (p) ?
Jawab :
Segitiga ABC dan segitiga CDE adalah segitiga yang sebangun, karena sudut
yang bersesuaian sama besar, sehingga dapat dilakukan perbandingan :Perhatikan gambarnya!
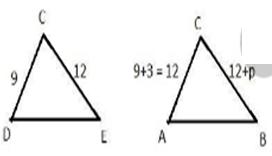
AD = 3 cm
CD = 9 cm
CE = 12 cm
BE = p cm
AC = AD + CD = 3 + 9 = 12 cm
BC = BE + CE = (p + 12) cm
Untuk segitiga yang sebangun berlaku perbandingan sisi :
CD/AC = CE/BC = DE/AB
9 : 12 = 12 : (p+12)
Kemudian kita lakukan kali silang
9 x (p + 12) = 12 x 12
9p + 108 = 144
9p = 144 - 108
9p = 36
p = 36/9
p = 4 cm
∴ Jadi nilai p adalah 4 cm- Perhatikan gambar berikut.
Tentukan nilai x.
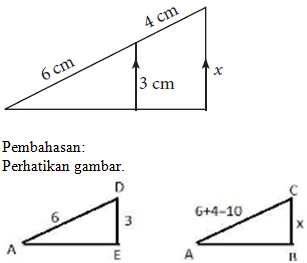
Diketahui :
AD = 6 cm
CD = 4 cm
DE = 3 cm
Ditanyakan : Nilai BC (x) ?
Jawab :
Segitiga ABC sebangun dengan segitiga AED karena sudut yang bersesuaian sama besar
AD = 6 cm
CD = 4 cm
DE = 3 cm
BC = x cm
AC = AD + CD = 6 + 4 = 10 cm
Untuk segitiga yang sebangun berlaku perbandingan sisi :
AD/AC = AE/AB = ED/BC
6 : 10 = 3 : x
Lalu kita lakukan kali silang
6x = (3)(10)
6x = 30
x = 30/6
x = 5 cm
∴ Jadi nilai x adalah 5 cm- Perhatikan gambar berikut
Tentukan nilai x dan y.
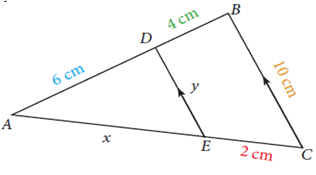
Pembahasan:
Diketahui :
AD = 6 cm
BD = 4 cm
CE = 2 cm
BC = 10 cm
Ditanyakan :
x = ... ?
y = ... ?
Jawab :
Mencari nilai x
- Perhatikan gambar berikut
Tentukan panjang AB.
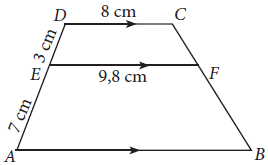
Pembahasan:
Buat garis yang sejajar dengan DA dari titik C sehingga memotong garis EF
di G dan memotong garis AB di H
(Untuk lebih jelasnya, lihat gambar di bawah)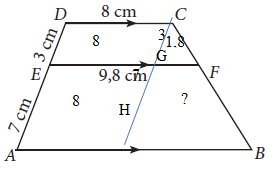
Sehingga diperoleh
DC = EG = AH = 8 cm
DE = CG = 3 cm
EA = GH = 7 cm
GF = EF - EG
GF = 9,8 - 8
GF = 1,8 cm
Perhatikan segitiga CHB, berlaku perbandingan kesebangunan :
GF/HB = CG/CH
1,8 : HB = 3 : 10
3HB = 1,8 (10)
3HB = 18
HB = 6
Jadi panjang AB adalah :
AB = AH + HB
AB = 8 cm + 6 cm
AB = 14 cm- Diketahui titik E, F, dan G pada trapesium ABCD. Sisi FE sejajar
dengan sisi AB. Jika AB = 7, DC = 14, DG = 8, FG = 4, GB = x , dan
GE = y , maka nilai x + y adalah …
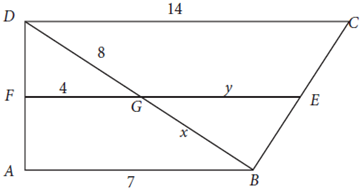
Pembahasan:
Diketahui :
Trapesium ABCD.
Sisi FE sejajar dengan sisi AB.
AB = 7
DC = 14,
DG = 8,
FG = 4,
GB = x,
GE = y
Ditanyakan :
Nilai x + y = ... ?
Jawab:
Mencari x
Perhatikan gambar di bawah: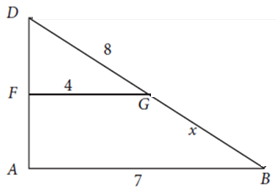
PEM
Perhatikan segitiga ∆ DFG sebangun ∆ DAB, berlaku perbandingan kesebangunan :
DG/DB = FG/AB
8 : (8+x) = 4 : 7
4(8 + x) = 8 × 7
32 + 4x = 56
4x = 56 – 32
4x = 24
x = 24/4
x = 6
Jadi panjang x = BG = 6
Mencari y
Perhatikan gambar di bawah: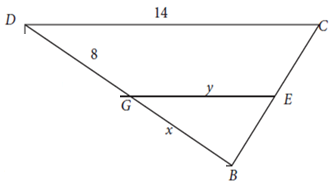
Perhatikan segitiga ∆ BEG sebangun ∆ BCD, berlaku perbandingan kesebangunan :
BG/BD = EG/CD
6 : 14 = y : 14
14 × y = 6 × 14
14y = 84
y = 84/14
y = 6
Panjang y = GE = 6
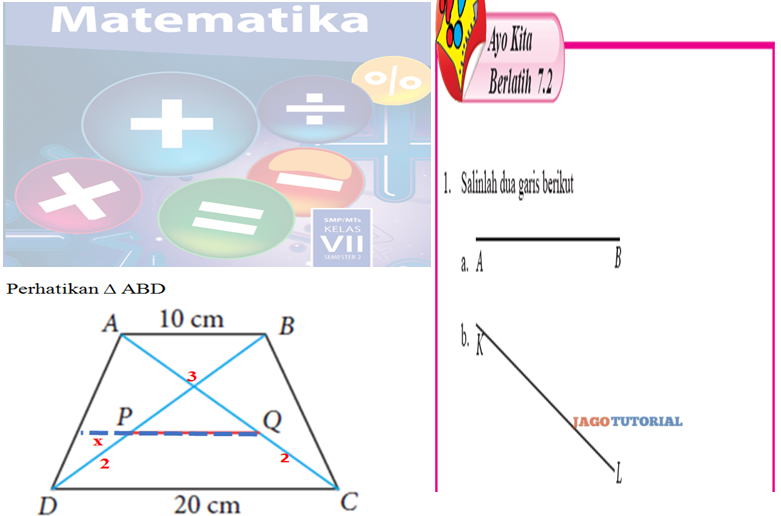
Jadi x + y = 6 + 6 = 12- Perhatikan gambar berikut.
Diketahui Trapesium ABCD, dengan AB//DC//PQ. Jika perbandingan
AQ : QC = BP : PD = 3 : 2. Tentukan panjang ruas garis PQ
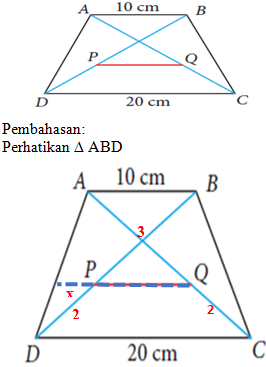
AB/x = BD/PD
AB/x = BD/DP
10/x = (2+3)/2
x(2+3) = 10 × 2
5x = 20
x = 20/5
x = 4
Perhatikan ∆ ADC
DC / (PQ + x) = AC/AQ
20 / (PQ + 4) = (3+2) / 3
5(PQ + 4) = 20 × 3
PQ + 4 = 60/5
PQ + 4 = 12
PQ = 12 - 4
PQ = 8 cm
Jadi panjang ruas garis PQ = 18 cm