
- Perhatikan gambar di bawah. Panjang AB = … cm
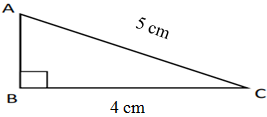
Pembahasan :
AB² = AC² – BC²
AB² = 5² – 4²
AB² = 25 – 16
AB² = 9
AB = √9
AB = 3 cm - Panjang hipotenusa dan tinggi suatu segitiga siku-siku berturut-turut adalah 20 cm
dan 16 cm. luas segitiga tersebut adalah …
Pembahasan:
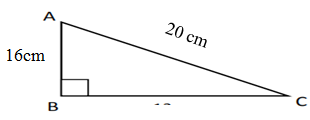
Mencari panjang BC
BC² = AC² – AB²
BC² = 20² – 16²
BC² = 400 – 256
BC² = 144
BC = √144
BC = 12 cm
Jadi luas segitiga tersebut adalah
= ½ × alas × tinggi
= ½ × BC × AB
= ½ × 12 × 16
= 6 × 16
= 96 cm²- Diketahui tiga bilangan berikut 6, 8, 10. Apakah merupakan tripel Pythagoras ?
Pembahasan :
a² + b² = c² rumus Pythagoras
6² + 8² = 10²
36 + 64 = 100
100 = 100
Jadi tiga bilangan berikut 6, 8, 10.
merupakan tripel Pythagoras
- Diketahui ukuran sisi-sisi segitiga sebagai berikut.
(i) 3 cm, 5 cm, 6 cm
(ii) 5 cm, 12 cm, 13 cm
(iii). 16 cm , 24 cm dan 32 cm
(iv). 20 cm , 30 cm dan 34 cm
Ukuran sisi yang membentuk segitiga lancip adalah …
Pembahasan :
Menentukan jenis segitiga :
- Jika a ≤ b < c dan c² < a² + b² → segitiga lancip
- Jika a ≤ b < c dan c² > a² + b² → segitiga tumpul
- Jika a ≤ b < c dan c² = a² + b² → segitiga siku-siku
(i) 3 cm , 5 cm dan 6 cm
6² > 3² + 5²
36 > 9 + 25
36 > 34
Jadi jenis segitiganya adalah segitiga tumpul,
karena c² > a² + b²
(ii) 5 cm , 12 cm dan 13 cm
13² = 5² + 12²
169 = 25 + 144
169 = 169
Jadi jenis segitiganya adalah segitiga siku-
siku, karena c² = a² + b²
(iii) 16 cm , 24 cm dan 32 cm
32² > 16² + 24²
1024 > 256 + 576
1024 > 832
Jadi jenis segitiganya adalah segitiga tumpul,
karena c² > a² + b²
(iv) 20 cm , 30 cm dan 34 cm
34² < 20² + 30²
1156 < 400 + 900
1156 < 1300
Jadi jenis segitiganya adalah segitiga lancip,
karena c² < a² + b²
- Jika sebuah segitiga panjang alasnya 12 cm dan tingginya 5 cm maka keliling
segitiga tersebut adalah ….
Pembahasan:
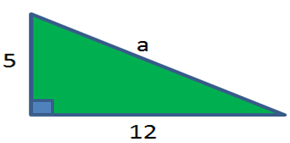
Mencari nilai a
a² = 12² + 5²
a² = 144 + 25
a² = 169
a = √169
a = 13
Jadi keliling segitiga adalah 12 + 5 + 13 = 30 cm6. Buktikan bahwa 6cm, 8cm, 10cm merupakan tripel pythagoras!
Pembahasan:
6² + 8² = 10²
36 + 64 = 100
100 = 100 terbukti- Perhatikan gambar segitiga istimewa berikut!
Tentukan panjang BC, AB dan AC
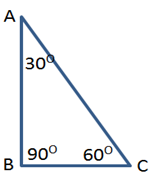
Pembahasan:
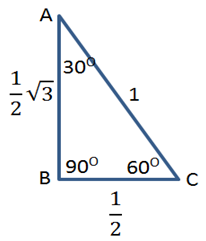
Jadi panjang BC = ½ dan AB = ½√3 dan AC = 1
- Suatu lingkaran diameternya 22 cm. Berapakah luas daerah lingkaran tersebut?
jika (π = 3,14).
Pembahasan:
Diketahui d = 22 cm dan π = 3,14
Ditanyakan: L
Jawab:
L = ¼ π d²
L = ¼ × 3,14 × 22 × 22
L = ¼ × 3,14 × 484
L = 3,14 × ¼ × 484
L = 3,14 × 121
L = 379,94
Jadi luas daerah lingkaran tersebut = 379,94 cm²- Keliling sebuah lingkaran adalah 88 cm.
Luas lingkaran tersebut adalah ….
Pembahasan :
Rumus
Luas Lingkaran = π r²
Keliling Lingkaran = 2 π r
Soal
Keliling lingkaran = 88 cm
Luas Lingkaran = …
Penyelesaian
88 cm = 2 × 22/7 × r
88 cm = 44/7 × r
r = 88 cm / 44/7
r = 88 × 7/44
r = 14 cm
Luas Lingkaran
=> 22/7 × 14 × 14
=> 22 × 2 × 14
=> 616 cm²
- Doni pergi ke sekolah menggunakan sepeda yang diameter rodanya 70 cm.
Dari rumah ke sekolah roda berputar sebanyak 1.000 kali. Jika π = 22/7, maka
jarak antara rumah Doni dan sekolah adalah ….
Pembahasan :
d roda = 70 cm
r = 1/2 d = 70 / 2 = 35 cm
K lingkaran = 2πr
K = 2 x 22/7 x 35
K = 220 cm
Roda berputar 1.000 kali, maka jaraknya:
= Keliling x 1.000
= 220 x 1000
= 220.000 cm atau 2,2 km
11.Di sebuah tempat akan dibuat sebuah taman berbentuk lingkaran dengan diameter
56 m. Di tengah taman tersebut, akan dibuat kolam berbentuk lingkaran dengan
diameter 28 m. Jika diluar kolam sampai tepi taman akan ditanami rumput dengan
biaya Rp6.000,00/m2 . Hitunglah seluruh biaya yang harus dikeluarkan untuk
menanam rumput tersebut !
Pembahasan:
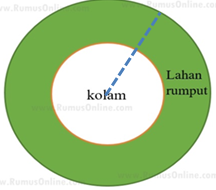
Diketahui : Diameter taman (d1) = 56 m
Diameter kolam (d2) = 28 m
Biaya = Rp6.000,00/m²
Ditanya : Seluruh biaya yg dikeluarkan untuk menanam rumput ?
Jawab:
Luas seluruh taman = ¼ π d²
Luas seluruh taman = ¼ × 22/7 × 56 × 56
Luas seluruh taman = 2464 m²
Luas kolam = ¼ π d²
Luas kolam = ¼ × 22/7 × 28 × 28
Luas kolam = 616 m²
Sehingga luas lahan rumput = 2464 m² – 616 m² = 1848 m²
Karena diketahui biaya tiap m² rumput adalah 6.000,00 maka biaya seluruh
penanaman rumput adalah luas lahan rumput kalikan biaya / m²
Biaya seluruhnya = 1848 x 6000 = 11.088.000
Jadi, seluruh biaya yg dikeluarkan untuk menanam rumput adalah Rp 11.088.000,00- Luas sebuah lingkaran adalah 1.256 cm². Hitunglah diameter lingkaran
jika π = 3,14
Pembahasan:
Diketahu : L = 1.256 cm² dan π = 3,14
Ditanyakan : diameter ?
Jawab :
Luas = ¼ π d²
1.256 = ¼ × 3,14 × d²
1256 / 3,14 = ¼ × d²
400 = ¼ × d²
d² = 400 : ¼
d² = 400 × 4
d² = 1600
d = √1600
d = 40 cm
Jadi diameter lingkaran adalah 40 cm.- Gambar berikut menunjukkan dua buah lingkaran dengan pusat P dan Q. panjang
jari-jari PR=12cm dan QS=5cm. RS adalah garis singgung persekutuan luar.
PQ=30cm, maka panjang RS adalah?
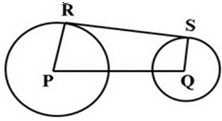
Pembahasan :
persekutuan luargaris singgung = RS
RS = √(PQ² – (PR – QS)²)
RS = √(30² – (12 – 5)²)
RS = √(900 – 49)
RS = √851 cm
RS = 29,17 cm
- Panjang jari-jari dua lingkaran adalah 11 cm dan 2 cm. Jika panjang garis
singgung persekutuan luarnya 12 cm maka tentukan jarak kedua pusat
lingkaran.
Pembahasan:
Diketahui: l = 12 cm , R = 11 cm, r = 2 cm
Ditanyakan p = ?
Jawab :
l = √(p² - (R-r)²)
l² = p² – (R - r)² keterangan: l jadi pangkat dan akar dihilangkan
12² = p² – (11 - 2)²
144 = p² – 81 maka p² = 144+81
p² = 225
p = √225 = 15 cm. Jadi, jarak kedua pusat lingkaran adalah 15 cm- Panjang garis singgung persekutuan dalam dua lingkaran adalah 24 cm dan
jarak kedua pusatnya adalah 26 cm. Jika panjang salah satu jari-jari lingkaran
6 cm. Hitunglah panjang jari-jari yang lain
Pembahasan:
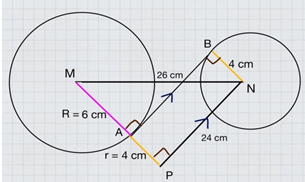
Perhatikan gambar terlampir.
Garis singgung persekutuan dalam AB digeser menjadi PN.
AB sejajar PN.
Jarak antar pusat adalah MN.
Misalkan,
jarak antar pusat = p, sebagai sisi miring
GSPD = d, dan total jari-jari (R + r), keduanya saling berpenyiku
Secara dalil Phytagoras, p² = d² + (R + r)²
Biasanya sering ditulis, d² = p² - (R + r)²
(R + r)² = p² - d²
(6 + r)² = 26² - 24²
Di sini kita coba mengingat salah satu tripel phytagoras yakni 5-12-13 yang
menjadi 10-24-26.
(6 + r)² = 10²
6 + r = 10
r = 10 - 6
Jadi panjang jari-jari yang lain sebesar r = 4 cm- Jika volume sebuah kubus 125 cm³, maka luas
permukaannya adalah ….
Pembahasan :
Diketahui volume sebuah kubus adalah 125 cm³.
V = s x s x s
⇔ V = s³
⇔ 125 = s³
⇔ s = ∛125
⇔ s = ∛5³
⇔ s = ∛125
⇔ s = 5
Jadi, sisi kubus tersebut adalah 5 cm.
Luas permukaan sebuah kubus adalah
L = 6 x luas bidang
⇔ L = 6 x (s x s)
⇔ L = 6 x s²
⇔ L = 6 x 5²
⇔ L = 6 x 25
⇔ L = 150
Jadi, luas permukaan kubus tersebut adalah 150 cm².
17. Diketahui luas permukaannya 96 cm². berapakah panjang rusuk kubus tersebut?
Jawab:
Luas Permukaan Kubus (LPK) = 6 × s²
96 = 6 × s²
s² = 96/6 = 16
s = √16
s = 4 cm
Jadi panjang rusuk kubus tersebut 4 cm- Sebuah balok memiliki volume 2430 cm³ dan memiliki panjang 18 cm serta
tinggi 9 cm. Berapakah lebar dari balok itu
Jawab:
Dik: V = 2430 cm³ , P = 18 cm dan t = 9 cm
Dit: l = ...?
V = p × l × t
2430 = 18 × l × 9
2430 = 162 . l
l = 2430/162 = 15
Jadi diperoleh kalau lebar dari balok itu adalah 15 cm- Diketahui luas permukan balok 220 cm² lebar 5 cm dan tingginya 4 cm. Berapa
panjang balok tersebut ?
Jawab:
Diketahui: L = 220 cm², l = 5 cm dan t = 4 cm
L = 2 x ( p x l + p x t + l x t )
220 = 2 x ( p x 5 + p x 4 + 5 x 4 )
220 = 2 x ( 5p + 4p + 20 )
220 = 2 x ( 9p + 20 )
220 = 18p + 40
18p = 220 – 40
18p = 180
p = 180/18 = 10 cm
Jadi panjang balok tersebut 10 cm.- Sebuah prisma alasnya berbentuk belah ketupat dengan panjang diagonal 16cm
dan 12 cm . tentukan tinggi prisma jika luas permukaannya adalah 672 cm²
Jawab:
Luas permukaan prisma = 672
2 (luas alas ) + ( kliling alas x t) = 672
2 (luas belah ketupat ) + ( kliling alas x t) = 672
2 ( (16 x 12) : 2) + ( 4 x 10 x t ) = 672
2 ( 96 ) + (40 x t) = 672
192 + 40 t = 672
40t = 672 - 192
40t = 480
t = 480/40
t = 12
Jadi tinggi prisma adalah 12 cm- Sebuah limas tegak alasnya berbentuk persegi panjang yang sisi-sisinya 9 cm
dan 16 cm. Puncak limas tepat berada di atas pusat alas dan tingginya 21 cm.
Hitunglah volume limas tersebut
Jawab:
Volume = 1/3 × Luas alas × Tinggi
Volume = 1/3 × (9 × 16) × 21
Volume = 7 × (9 × 16)
Volume = 7 × (144)
Volume = 1008 cm³
Jadi volume limas tersebut 1008 cm³- Perhatikan balok ABCD.EFGH berikut ini.
Tentukan panjang diagonal ruang CE.
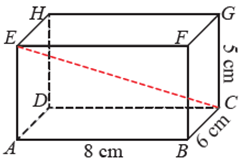
Jawab:
(CE)² = p² + l ² + t²
(CE)² = (CD)² + (AD)² + (AE)²
(CE)² = 8² + 6² + 5²
(CE)² = 64 + 36 + 25
(CE)² = 125
CE = √125
CE = √25 × √5
CE = 5√5
Jadi, panjang diagonal ruang CE adalah 5√5 cm23. Jangkauan interkuartil dari 7, 4, 5, 6, 7, 4, 5, 7, 8, 9, 6 adalah…
Pembahasan :
Urutkan data terlebih dahulu
4,4,5,5,6,6,7,7,7,8,9
Q1 = 5
Q2= 6
Q3 = 7
Qr = Q3 - Q1
= 7 - 5
= 2- Data penjualan beras dari toko sembako pada lima hari minggu pertama bulan
Januari adalah sebagai berikut
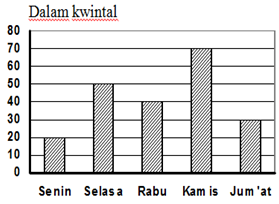
Rata-rata banyak beras yang terjual setiap hari pada minggu tersebut adalah ….
Jawab:
Rata-rata beras terjual = (20 + 50 + 40 + 70 + 30) / 5 = 210/5 = 42
Jadi Rata-rata banyak beras yang terjual setiap hari pada minggu tersebut
adalah 42 kwintal.- Dari suatu nilai ulangan matematika 15 siswa, diperoleh data 65,75,85,75,60,
80,80, 85,90,65,80,85,90,95,100. Nilai rata-rata ulangan matematika tersebut
adalah … .
Jawab:
Rata-rata = (65+75+85+75+60+ 80+80+ 85+90+65+80+85+90+95+100)/15
Rata-rata = 1210/15
Rata-rata = 80,67- Dari 18 siswa yang mengikuti ulangan Bahasa Inggris, nilai rata-ratanya 65.
Setelah 2 orang siswa ikut ulangan susulan, nilai rata-ratanya menjadi 64.
Nilai rata-rata 2 orang siswa yang ikut ulangan susulan adalah….
Jawab:
Jumlah nilai 18 siswa = 18 x 65 = 1170
Jumlah nilai 18 + 2 siswa = 20 x 64 = 1280
Jumlah nilai 2 siswa = 1280 - 1170 = 110
Nilai rata-rata ke-2 siswa itu adalah 110 : 2 = 5527. Tentukan median dari data pada tabel di bawah!

Jawab:
Mediannya = (data ke 20 + data ke 21) / 2
Mediannya = (6 + 7) / 2
Mediannya = 13/2 = 6,5
(Karena 40 data, jika diurutkan suku tengahnya adalah ke-20 dan 21)- Banyak siswa yang mendapat nilai lebih dari nilai rata-rata dari tabel di bawah
adalah ….

Jawab:
Rata-rata = (4×2 + 5×7 + 6×5 + 7×4 + 8×2) / (2+7+5+4+2)
Rata-rata = (8 + 35 + 30 + 28 + 16) / (20)
Rata-rata = (117) / (20)
Nilai rata-rata = 5, 85
Nilai lebih dari 5,85 yaitu nilai 6, 7 dan 8
Banyak siswa yang mendapat nilai lebih dari rata-rata= 5 + 4 + 2 = 11 orang.- Dua buah dadu dilambungkan bersama. Peluang muncul kedua mata dadu
bilangan prima adalah ….
Jawab:
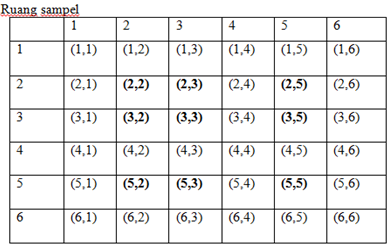
n(S) = 36
n(kedua mata dadu prima) = 9
Jadi peluang muncul kedua mata dadu berjumlah tujuh = 9/36 = ¼
- Suatu keluarga ingin memiliki 2 anak saja. Jika peluang lahir anak laki–laki
dan lahir anak perempuan sama, peluang kedua anaknya perempuan adalah …
Jawab:
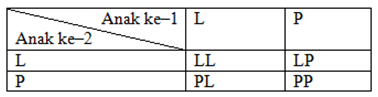
S= {LL,LP,PL,PP}
n(S) = 4
Peluang kedua anaknya perempuan = Peluang (PP) = ¼
Selamat belajar semoga bermanfaat







